2017年内蒙古巴彦淖尔市磴口县中考数学二模试卷
试卷更新日期：2017-07-25 类型：中考模拟
一、选择题
-
1. 9的算术平方根是（ ）A、±3 B、3 C、 D、2. 2016年，巴彦淖尔市计划投资42亿元，完成300个嘎查村的建设任务．农村牧区“十个全覆盖”推进正酣．将42亿用科学记数法应表示为（ ）A、0.042×107 B、0.42×108 C、4.2×109 D、42×10103. 下列计算正确的是（ ）A、a3+a2=2a5 B、（﹣2a3）2=4a6 C、（a+b）2=a2+b2 D、a6÷a2=a34. 不等式组 的整数解的和是（ ）A、﹣1 B、1 C、0 D、25. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（ ）
A、35° B、40° C、50° D、65°6. 一个几何体的三视图如图所示，该几何体的侧面积为（ ）
A、2πcm2 B、4πcm2 C、8πcm2 D、16πcm27. 已知一组数据：1，2，6，3，3，下列说法错误的是（ ）A、众数是3 B、中位数是6 C、平均数是3 D、方差是2.88. 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上．下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+ ．其中正确的个数为（ ）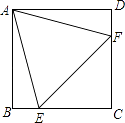
A、1 B、2 C、3 D、49. 如图，在平行四边形ABCD中，E是CD上的一点，DE：EC=2：3，连接AE、BE、BD，且AE、BD交于点F，则S△DEF：S△EBF：S△ABF=（ ）
A、2：5：25 B、4：9：25 C、2：3：5 D、4：10：2510.如图，矩形ABCD中，AB=1，BC=2，点P从点B出发，沿B→C→D向终点D匀速运动，设点P走过的路程为x，△ABP的面积为S，能正确反映S与x之间函数关系的图象是（ ）
A、
B、
C、
D、
二、填空题
-
11. 分解因式：﹣3x3y+12x2y﹣12xy= ．12. 要使式子 有意义，则a的取值范围为 ．13. 在一个不透明的袋子中装有若干个除颜色外形状大小完全相同的球，如果其中有3个白球，且摸出白球的概率是 ，那么袋子中共有球个．14.
如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为m（结果不作近似计算）．
15. 抛物线y=x2﹣2x+3的顶点坐标是 ， 当x 时，y随x的增大而减小．16.如图，△ABC是等腰直角三角形，AC=BC=a，以斜边AB上的点O为圆心的圆分别与AC，BC相切于点E，F，与AB分别交于点G，H，且EH的延长线和CB的延长线交于点D，则CD的长为 ．
三、解答题
-
17. 综合题。(1)、计算：2sin60°﹣（ ）﹣1+（ ﹣1）0(2)、先化简，再求值：（1﹣ ）÷ ，其中a=2+ ．18. 某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，并且篮球的单价比足球的单价多20元，请解答下列问题：(1)、求出足球和篮球的单价；(2)、若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？(3)、在（2）的条件下，若已知足球的进价为50元，篮球的进价为65元，则在第二次购买方案中，哪种方案商家获利最多？19. 某市为了增强学生体质，全面实施“学生饮用奶”营养工程．某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用．浠马中学为了了解学生对不同口味牛奶的喜好，对全校订购牛奶的学生进行了随机调查（每盒各种口味牛奶的体积相同），绘制了如图两张不完整的人数统计图：
(1)、本次被调查的学生有名；(2)、补全上面的条形统计图1，并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数；(3)、该校共有1200名学生订购了该品牌的牛奶，牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶．要使学生每天都喝到自己喜好的口味的牛奶，牛奶供应商每天送往该校的牛奶中，草莓味要比原味多送多少盒？20.如图有A、B两个大小均匀的转盘，其中A转盘被分成3等份，B转盘被分成4等份，并在每一份内标上数字．小明和小红同时各转动其中一个转盘，转盘停止后（当指针指在边界线时视为无效，重转），若将A转盘指针指向的数字记作一次函数表达式中的k，将B转盘指针指向的数字记作一次函数表达式中的b．
(1)、请用列表或画树状图的方法写出所有的可能；(2)、求一次函数y=kx+b的图象经过一、二、四象限的概率．21. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．
(1)、证明：四边形ACDE是平行四边形；(2)、若AC=8，BD=6，求△ADE的周长．22. 如图，已知A（﹣4， ），B（﹣1，2）是一次函数y=kx+b与反比例函数 （m≠0，m＜0）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D．
(1)、根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？(2)、求一次函数解析式及m的值；(3)、P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标．23. 如图，⊙O是Rt△ABC的外接圆，AC是⊙O的直径，弦BD=BA，AB=12，BC=5，BE⊥DC，交DC的延长线于点E．
(1)、求证：△ABC∽△DEB；(2)、求证：BE是⊙O的切线；(3)、求DE的长．24.已知，如图二次函数y=ax2+bx+c（a≠0）的图象与y轴交于点C（0，4）与x轴交于点A、B，点B（4，0），抛物线的对称轴为x=1．直线AD交抛物线于点D（2，m）．
(1)、求二次函数的解析式并写出D点坐标；(2)、点E是BD的中点，点Q是线段AB上一动点，当△QBE和△ABD相似时，求点Q的坐标；(3)、抛物线与y轴交于点C，直线AD与y轴交于点F，点M为抛物线对称轴上的动点，点N在x轴上，当四边形CMNF周长取最小值时，求出满足条件的点M和点N的坐标．