2017年江西省宜春市中考数学模拟试卷（4月份）

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

1. 2017年春节黄金周宜春市共接待游客2234000人次，将2234000用科学记数法表示为（）

A、 22.34×10⁵ B、2.234×10⁵ C、2.234×10⁶ D、0.2234×10⁷

查看试题解析
2. 下列计算正确的是（）

A、3a﹣2a=1 B、a⁶÷a²=a³ C、（2ab）³=6a³b³ D、﹣a⁴•a⁴=﹣a⁸

查看试题解析
3. 由一个圆柱体与一个长方体组成的几何体如图，这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 在反比例函数y= $\frac{1 - k}{x}$ 的图象的任一支上，y都随x的增大而增大，则k的值可以是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
5. 如图，四边形ABCD内接于⊙O，F是 $\hat{C D}$ 上一点，且 $\hat{D F}$ = $\hat{B C}$ ，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=30°，则∠E的度数为（）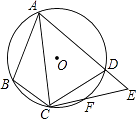

A、45° B、50° C、55° D、60°

查看试题解析
6. 对于每个非零自然数n，抛物线y=x²﹣ $\frac{2 n + 1}{n (n + 1)}$ x+ $\frac{1}{n (n + 1)}$ 与x轴交于A_n、B_n两点，以A_nB_n表示这两点间的距离，则A₁B₁+A₂B₂+…+A₂₀₁₇B₂₀₁₇的值是（）

A、 $\frac{2015}{2016}$ B、 $\frac{2016}{2017}$ C、 $\frac{2017}{2018}$ D、1

查看试题解析

二、填空题

7. 化简： $\sqrt{18} - \sqrt{8}$ = ．

查看试题解析
8. 若关于x，y的二元一次方程组 ${\begin{matrix} 2 x + y = - 3 k + 1 \\ x + 2 y = 2 \end{matrix}$ 的解满足x+y＞2，则k的取值范围是．

查看试题解析
9. 一组数据1，3，2，5，2，a的众数是a，这组数据的中位数是．

查看试题解析
10. 若关于x的方程x²+（k﹣2）x+k²=0的两根互为倒数，则k= ．

查看试题解析
11. 如图，某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框，则所得扇形的面积的最大值为．

查看试题解析
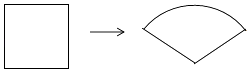12.
如图，平面直角坐标系中，已知点A（8，0）和点B（0，6），点C是AB的中点，点P在折线AOB上，直线CP截△AOB，所得的三角形与△AOB相似，那么点P的坐标是．

查看试题解析

三、解答题

13. 综合题。

(1)、计算：（ $\sqrt{3}$ ﹣1）⁰+2sin30°﹣（ $\frac{1}{2}$ ）^﹣¹+|﹣2017|；

(2)、如图，在△ABC中，已知∠ABC=30°，将△ABC绕点B逆时针旋转50°后得到△A₁BC₁ ，若∠A=100°，求证：A₁C₁∥BC．

查看试题解析
14. 解分式方程： $\frac{2}{x + 3}$ + $\frac{1}{3 - x}$ = $\frac{1}{x^{2} - 9}$ ．

查看试题解析
15. 如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标为（﹣4，8），对角线AC⊥x轴于点C，点D在y轴上，求直线AB的解析式．

查看试题解析
16. 菲尔兹奖是国际上享有崇高声誉的一个数学奖项，每4年评选一次，颁给有卓越贡献的年轻数学家，被视为数学界的诺贝尔奖．下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄（岁）：
39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据，解答以下问题：

(1)、小彬按“组距为5”列出了如下的频数分布表，每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图：
分组
频数
A：25～30
B：30～35
15
C：35～40
31
D：40～45
总计
50

(2)、在（1）的基础上，小彬又画出了如图所示的扇形统计图，图中B组所对的圆心角的度数为；

(3)、根据（1）中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征．

查看试题解析
17. 如图，▱ABCD的顶点A、B、D均在⊙O上，请仅用无刻度的直尺按要求作图．

(1)、AB边经过圆心O，在图（1）中作一条与AD边平行的直径；

(2)、AB边不经过圆心O，DC与⊙O相切于点D，在图（2）中作一条与AD边平行的弦．

查看试题解析
18. 近年来，手机微信红包迅速流行起来．去年春节，小米的爷爷也尝试用微信发红包，他分别将10元、30元、60元的三个红包发到只有爷爷、爸爸、妈妈和小米的微信群里，他们每人只能抢一个红包，且抢到任何一个红包的机会均等（爷爷只发不抢，红包里钱的多少与抢红包的先后顺序无关）．

(1)、求小米抢到60元红包的概率；

(2)、如果小米的奶奶也加入“抢红包”的微信群，他们四个人中将有一个人抢不到红包，那么这种情况下，求小米和妈妈两个人抢到红包的钱数之和不少于70元的概率．

查看试题解析
19. 如图（1），A₁B₁和A₂B₂是水面上相邻的两条赛道（看成两条互相平行的线段）．甲是一名游泳运动健将，乙是一名游泳爱好者，甲在赛道A₁B₁上从A₁处出发，到达B₁后，以同样的速度返回A₁处，然后重复上述过程；乙在赛道A₂B₂上以1.5m/s的速度从B₂处出发，到达A₂后以相同的速度回到B₂处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两人同时出发，设离开池边B₁B₂的距离为y（m），运动时间为t（s），甲游动时，y（m）与t（s）的函数图象如图2所示．

(1)、赛道的长度是 m，甲的速度是 m/s；当t=s时，甲、乙两人第一次相遇，当t=s时，甲、乙两人第二次相遇？

(2)、第三次相遇时，两人距池边B₁B₂多少米．

查看试题解析
20. 如图（1）是一个晾衣架的实物图，支架的基本图形是菱形，MN是晾衣架的一个滑槽，点P在滑槽MN上、下移动时，晾衣架可以伸缩，其示意图如图（2）所示，已知每个菱形的边长均为20cm，且AB=CD=CP=DM=20cm．

(1)、当点P向下滑至点N处时，测得∠DCE=60°时
①求滑槽MN的长度；
②此时点A到直线DP的距离是多少？

(2)、当点P向上滑至点M处时，点A在相对于（1）的情况下向左移动的距离是多少？
（结果精确到0.01cm，参考数据 $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
21. 如图，在平面直角坐标系中，△ABC内接于⊙P，AB是⊙P的直径，A（﹣1，0）C（3，2 $\sqrt{2}$ ），BC的延长线交y轴于点D，点F是y轴上的一动点，连接FC并延长交x轴于点E．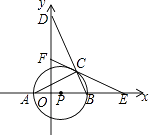

(1)、求⊙P的半径；

(2)、当∠A=∠DCF时，求证：CE是⊙P的切线．

查看试题解析
22.
如图，在平面直角坐标系中，已知点A（﹣2，﹣4），直线x=﹣2与x轴相交于点B，连接OA，抛物线y=﹣x²从点O沿OA方向平移，与直线x=﹣2交于点P，顶点M到点A时停止移动．

(1)、线段OA所在直线的函数解析式是；

(2)、设平移后抛物线的顶点M的横坐标为m，问：当m为何值时，线段PA最长？并求出此时PA的长．

(3)、若平移后抛物线交y轴于点Q，是否存在点Q使得△OMQ为等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析
23.
阅读理解
如图（1），在正多边形A₁A₂A₃…A_n的边A₂A₃上任取一不与点A₂重合的点B₂ ，并以线段A₁B₂为边在线段A₁A₂的上方作以正多边形A₁B₂B₃…B_n ，把正多边形A₁B₂B₃…B_n叫正多边形A₁A₂…A_n的准位似图形，点A₃称为准位似中心．
特例论证

(1)、
如图（2）已知正三角形A₁A₂A₃的准位似图形为正三角形A₁B₂B₃ ，试证明：随着点B₂的运动，∠B₃A₃A₁的大小始终不变．

(2)、
如图（3）已知正方形A₁A₂A₃A₄的准位似图形为正方形A₁B₂B₃B₄ ，随着点B₂的运动，∠B₃A₃A₄的大小始终不变？若不变，请求出∠B₃A₃A₄的大小；若改变，请说明理由．

(3)、在图（1）的情况下：
①试猜想∠B₃A₃A₄的大小是否会发生改变？若不改变，请用含n的代数式表示出∠B₃A₃A₄的大小（直接写出结果）；若改变，请说明理由．
①∠B₃A₃A₄+∠B₄A₄A₅+∠B₅A₅A₆+…+∠B_nA_nA₁= $\underline{}$ （用含n的代数式表示）

查看试题解析

分组	频数
A：25～30
B：30～35	15
C：35～40	31
D：40～45
总计	50