广东省湛江市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-12 类型：期中考试
一、选择题：(共15小题，每小题2分，满分30分)
-
1. 下列平面图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列图形具有稳定性的是（ ）A、六边形 B、五边形 C、平行四边形 D、等腰三角形3. 下列图形中，对称轴最多的是（ ）A、等边三角形 B、矩形 C、正方形 D、圆4. 点M(3，-2)关于x轴对称的对称点的坐标是（ ）A、(-3，2) B、(3，2) C、(-3，-2) D、(2，3)5. 如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点0，测得OA=15米，OB=10米，A、B间的距离不可能是（ ）米。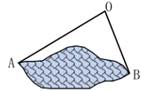
A、25 B、20 C、15 D、106. 能把一个三角形分成两个面积相等的三角形是三角形的（ ）A、中线 B、高线 C、角平分线 D、以上都不对7. 如图，亮亮书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画了一个与书上完全一样的三角形，那么亮亮画图的依据是（ ）。
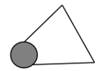A、SSS B、SAS C、ASA D、AAS8. 如果三角形的两边长分别为3和5，则第三边L的取值范围是（ ）A、2<L<15 B、L<8 C、2<L<8 D、10<L<169. 已知△ABC≌△DEF，∠A=70°，∠E=30°，则∠F的度数为（ ）A、80° B、70° C、30° D、100°10. 点P在∠AOB的平分线上，点P到OA边的距离等于5，点Q是OB边上的任意一点，则下列选项正确的是（ ）A、PQ>5 B、PQ<5 C、PQ≥5 D、PQ≤511. 如图，△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，则∠BDC的度数为（ ）
A、72 B、36° C、60° D、82°12. 在△ABC中，已知∠A：∠B：∠C=1：2：3，则三角形的形状是（ ）A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定13. 一个正多边形的每个外角都等于60°，那么它是（ ）A、正十二边形 B、正十边形 C、正八边形 D、正六边形14. 如图，已知AB⊥BC，BC⊥CD，AB=DC，可以判定△ABC≌△DCB，判定的根据是（ ）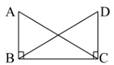
A、HL B、ASA C、SAS D、AAS15. 等腰三角形的两边长分别为5和11，则它的周长为（ ）A、27 B、21或27 C、25 D、21二、填空题：(本大题共10小题，每小题3分，满分30分)
-
16. 等边三角形的每个内角为度。17. 已知点P(2，3)，点A与点P关于y轴对称，则点A的坐标是 。18. 如图，木工师傅做完门框后，为了防止变形，常常像右图中所示那样钉上两条斜拉的木条，这样做的数学道理是 。
19. 如图，△ABC≌△DEF，则∠F=。
20. 已知一个三角形的三边长a、b、c，满足(a-b)2+|b-c|=0，则这个三角形是 三角形。21. 如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米又向左转30°，回到A点时一共走了米。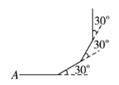
22. 一个多边形的内角和等于外角和的2倍，则这个多边形的边数是。23. 如图，点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB，垂足分别是E和F，若PE=3，则PE=。
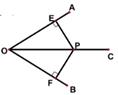24. 如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为cm2。
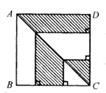25. 如图是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔．若一个球按图中所示的方向被击出(球可以经过多反射)，则该球最后将落入的球袋是。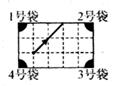
三、解答题(一)：(本大题共3小题，每小题6分，满分18分)
-
26. 求出图中的x的值。
27. 在△ABC中，已知∠A=30°，∠B=2∠C，求∠B和∠C的度数。28. 已知：如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等．(不用写作法，但要保留作图痕迹)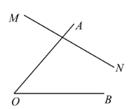
四、解答题(二)：(本大题共3小题，每小题6分，满分18分)
-
29. 已知：如图(没图)，A、C、F、D在同一直线上，AF=DC，AB=DE，BC=EF，求证：△ABC≌△DEF
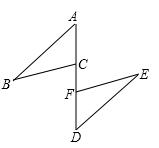30. 已知：a，b，c为△ABC的三边长，且2a2+2b2+2c2=2ab+2ac+2bc，试判断△ABC的形状，并证明你的结论。31. 如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是28cm2 ， AB=20cm，AC=8cm，求DE的长．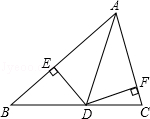
五、解答题(三)：(本大题共3小题，每小题8分，满分24分)
-
32.(1)、在图所示编号为①、②、③、④的四个三角形中，关于x轴对称的两个三角形编号为 ；关于y轴对称的两个三角形编号为；
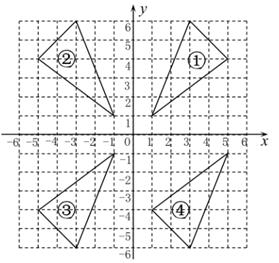(2)、写出图中△ABC三个顶点的坐标：A( ， )、B（ ， ）、C（ ， ）
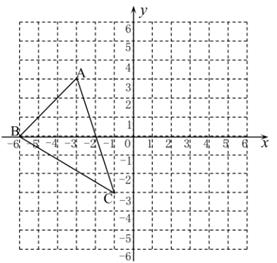(3)、在图中作出△ABC关于y轴对称的△A1B1C1(不写作法)。 33. 数学中的对称美、统一美、和谐美随处可见，在数的运算中就有一些有趣的对称形式。(1)、我们发现：12=1，112=-121，1112=12321，11112=1234321，…请你根据发现的规律，接下去再写两个等式；(2)、对称的等式：12×231=132×21．仿照这一形式，完成下面的等式，并进行验算：12×462= ， 18×891=。34. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E。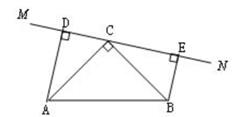
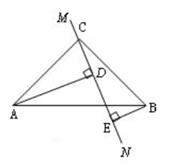(1)、当直线MN绕点C旋转到图的位置时，求证：①△ADC≌△CEB；②DE=AD+BE。
(2)、当直线MN绕点C旋转到图的位置时，DE、AD、BE三条线段的长度关系又如何?并说明理由。