浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算提高训练

试卷更新日期：2019-12-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 一个两位数，个位数字为a ，十位数字比个位数字大1，则这个两位数可表示为（）

A、11a－1 B、11a＋1 C、11a＋10 D、11a－10

查看试题解析
2. 如图(1)，在边长为 $a$ 的大正方形中，剪去一个边长为 $b (a > b)$ 的小正方形，然后将余下的部分剪开拼成长方形，如图(2)，若大正方形的周长为 $c_{1} ，$ 长方形的周长为 $c_{2} ，$ 则 $c_{1}$ 与 $c_{2}$ 的大小关系是（）

A、 $c_{1} > c_{2}$ B、 $c_{1} = c_{2}$ C、 $c_{1} < c_{2}$ D、不能确定

查看试题解析
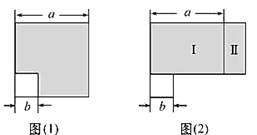3. 已知 $| m | = 2$ ， $| n | = 5$ ，且 $| m - n | = n - m$ ，则 $m + n$ 的值是（）

A、7 B、3 C、-3或-7 D、3或7

查看试题解析
4. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4} \neq 0$ ，则 $\frac{2 a - b}{c} =$ （）

A、 $\frac{1}{4}$ B、 $- \frac{1}{4}$ C、2 D、 $\frac{1}{2}$

查看试题解析
5. 某同学把4×(□-3)错抄写成了4×□-3，抄错后的答案为y，正确答案为x，则x-y的值为（）

A、-15 B、-12 C、-9 D、0

查看试题解析
6. 已知 $2 a^{x + 2} b$ 与 $- \frac{2}{3} a^{5} b^{3 y - 2}$ 是同类项，则 $| x - 5 y |$ 等于（）

A、 B、1 C、2 D、-2

查看试题解析
7. 五个连续偶数，中间一个是 2n (n 为正整数)，那么这五个数的和是（）．

A、10n ； B、10n + 10 ； C、5n + 5 ； D、5n ．

查看试题解析
8. 下列说法：①若两个数互为倒数，则它们的乘积为1；②若a、b互为相反数，则 $\frac{b}{a}$ ＝－1；③多项式 $2 x^{2} + 3 y^{2}$ 的次数为4；④若a为任意有理数，则 $a - | a |$ ≤0，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如果xy^|a|- $\frac{1}{3}$ (a-2)y²+1是三次二项式，则a的值为（）

A、2 B、-3 C、±2 D、±3

查看试题解析
10. 把六张大小形状完全相同的小平行四边形卡片（如图）放在一个底面为平行四边形的盒子底部，两种放置方法如图2、图3所示，其中3中的重叠部分是平行四边形EFGH，若EH＝2GH，且图2中阴影部分的周长比图3中阴影部分的周长大3.则AB﹣AD的值为（）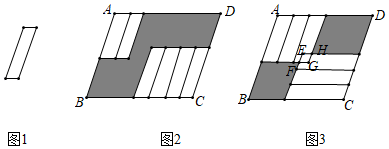

A、0.5 B、1 C、1.5 D、3

查看试题解析

二、填空题

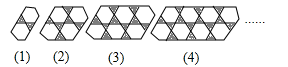
11. 如图所示，在由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案中，第5个图形中阴影小三角形的个数是，第n个图形中阴影小三角形的个数是.

查看试题解析
12. 已知当 x = -2 时，代数式 $a x^{5} + b x + 1$ 的值为 99 ，那么当 x = 2 时，代数式 $a x^{5} + b x + 1$ 的值是.

查看试题解析
13. 已知 $a$ , $b$ 互为相反数, $c$ , $d$ 互为倒数, $| m | = 2$ ,则 $a + c d + b - 3 m =$ .

查看试题解析
14. 如图是一个长方形的储物柜，它被分成大小不同的正方形①②③④和一个长方形⑤.若要计算长方形⑤的周长，则只需要知道哪个小正方形的周长？你的选择是正方形（填编号）.

查看试题解析
15. 实数a、b、c在数轴上的位置如图所示，化简 $\sqrt{{(a + b)}^{2}} - | b - c | + \sqrt{{(a - b)}^{2}}$ 的结果为.

查看试题解析
16. 关于x的多项式 $x^{4} + {mx}^{3} - x$ 与多项式 $2 x^{3} - 6 x^{2} + nx - 3$ 的和不含三次项和一次项，则代数式 ${(m + n)}^{2018}$ 的值为.

查看试题解析

三、解答题

17. 先化简，再求值．

(1)、6a²－5a（a+2b－1）+a（－a+10b）+5，其中a＝－1，b＝2008；

(2)、3xy²﹣[xy﹣2（2xy﹣ $\frac{3}{2}$ x²y）+2xy²]+3x²y，其中x、y满足（x+2）²+|y﹣1|=0．

查看试题解析
18. 已知 $a, b$ 是实数，且有 $| a - \sqrt{2} + 1 | 和 {(b + \sqrt{2})}^{2}$ 互为相反数，求 $2 a - b$ 的值.

查看试题解析
19. 已知a+2是1的平方根,3是b-3的立方根， $\sqrt{6}$ 的整数部分为c，求a+b+c的值

查看试题解析
20. 已知a、b、c的大小为0<c<1，b<-1，a<b；化简：｜a＋c｜＋2｜b＋c｜－3｜a＋b｜.

查看试题解析
21. ①已知﹣5x³y^|a|﹣（a﹣5）x﹣6是关于x、y的八次三项式，求a²﹣2a+1的值.
②对于有理数a、b定义一种运算： $a \oplus b = - 2 a + b$ ，计算 $- 2 \oplus 1 + 4$ 的值.

查看试题解析
22. 观察下列三行数：
−2，4，−8，16，−32， $a_{n}$

$- \frac{1}{2}$ ，1，−2，4，−8， $b_{n}$

−1，5，−7，17，−31， $c_{n}$

如图，第一行数的第n(n为正整数)个数 $a_{n}$ 用来表示，第二行数的第n个数用 $b_{n}$ 来表示，第三行数的第n个数用 $c_{n}$ 来表示

(1)、根据你发现的规律，请用含n的代数式表示数 $a_{n}$ ， $b_{n}$ ， $c_{n}$ 的值 $a_{n}$ =； $b_{n}$ =； $c_{n}$ =；

(2)、取每行的第6个数，计算这三个数的和

(3)、若 $a_{n}$ 记为x，求 $a_{n} + b_{n} + c_{n}$ (结果用含x的式子表示并化简)

查看试题解析
23. 阅读下面材料：
在数轴上2与﹣1所对的两点之间的距离：|2﹣(﹣1)|=3；

在数轴上﹣2与3所对的两点之间的距离：|﹣2﹣3|=5；

在数轴上﹣3与﹣1所对的两点之间的距离：|(﹣1)﹣(﹣3)|=2

归纳：在数轴上点A、B分别表示数a、b，则A、B两点之间的距离AB=|a﹣b|或|b﹣a|

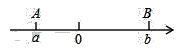
回答下列问题：

(1)、数轴上表示数x和1的两点之间的距离表示为；数轴上表示数x和的两点之间的距离表示为|x+2|；

(2)、请你在草稿纸上画出数轴，当表示数x的点在﹣2与3之间移动时，|x﹣3|+|x+2|的值总是一个固定的值为：．

(3)、继续请你在草稿纸上画出数轴，探究当x=时，|x-3|+|x+2|=7.

查看试题解析
24. 我们自从有了用字母表示数，发现表达有关的数和数量关系更加简洁明了，从而更助于我们发现更多有趣的结论，请你按要求试一试。

(1)、用代数式表示：
① $a$ 与 $b$ 的差的平方；② $a$ 、 $b$ 两数的平方和与 $a$ ， $b$ 两数积的2倍的差；

(2)、当 $a$ ＝3， $b$ ＝－2时，求第(1)题中①②所列的代数式的值；

(3)、由第(2)题的结果，你发现了什么等式？

(4)、利用你发现的结论：求2018²－2×2018×2017＋2017²的值．

查看试题解析

浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算 提高训练

一、单选题

二、填空题

三、解答题

浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算提高训练