浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算基础巩固

试卷更新日期：2019-12-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 若一个正方形的边长是 $m$ ，则这个正方形的周长是（）

A、 $4 m$ B、 $m + 4$ C、 $m^{2}$ D、 $m^{4}$

查看试题解析
2. “ $a$ 的2倍与3的和”用式子表示是（）

A、 $2 a - 3$ B、 $2 a + 3$ C、 $2 (a + 3)$ D、 $3 a + 2$

查看试题解析
3. 如图，三角尺（阴影部分）的面积是（）

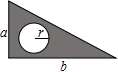A、ab－2πr B、 $\frac{1}{2}$ ab－πr² C、ab－πr² D、 $\frac{1}{2}$ ab－2πr

查看试题解析
4. 不是同类项的一对式子是（）

A、 $3 a b$ 与 $2 a b$ B、 $3 a^{2} b$ 与 $- \frac{1}{2} b a^{2}$ C、 $3 a$ 与 $2 a b$ D、 $\frac{1}{3}$ 与 $- \frac{1}{2}$

查看试题解析
5. 某商品的原价是每件x元，在销售时每件加价20元，再降价15%，则现在每件的售价是（）元.

A、15%x+20 B、（1﹣15%）x+20 C、15%（x+20） D、（1﹣15%）（x+20）

查看试题解析
6. 下列各式计算正确的是（）

A、2a+3b=5ab B、3a²+2a³=5a⁵ C、6ab-ab=5ab D、5+a=5a

查看试题解析
7. 下列叙述正确的是（）

A、 $x$ 的系数是0，次数为1 B、单项式 $∴ g (x) > g (0) = 0$ 的系数为1，次数是6 C、 $5 x^{2} y$ 和 $- 2 y x^{2}$ 不是同类项 D、多项式 $2 x^{2} - 3 x - 5$ 次数为2，常数项为5

查看试题解析
8. 下列代数式添括号正确的是（）

A、a+b+2=a+(b-2) B、a-b-1=a-(b-1) C、a+b-1=a+(b+1) D、a-b+1=a-(b-1)

查看试题解析
9. 已知 $x - 2 y = 2$ ，则 $3 - 2 x + 4 y$ 的值是（）

A、−1 B、1 C、5 D、7

查看试题解析
10. 已知关于 $x$ ， $y$ 的多项式 $3 x^{2} - 2 (y - x^{2} - 1) + m x^{2}$ 的值与 $x$ 无关,则 $m$ 的值为（）

A、 $0$ B、 $- 3$ C、 $- 5$ D、 $1$

查看试题解析

二、填空题

11. 已知多项式3a⁴b^m﹣a²b+1是六次三项式，则m＝．

查看试题解析
12. 已知2x²yⁿ与-6x^my是同类项，则m+n=。

查看试题解析
13. 若单项式－5x²y^a与－2x^by⁵的和仍为单项式，则这两个单项式的和为

查看试题解析
14. 已知 $a$ 、 $b$ 互为相反数， $c$ 、 $d$ 互为倒数，则 $a + b - c d =$ .

查看试题解析
15. 当 $m =$ 时，多项式 $3 x^{2} + 2 x y + y^{2} - m x^{2}$ 中不含 $x^{2}$ 项．

查看试题解析
16. 已知长方形的长、宽分别为x，y，周长为12，面积为4，则x²+y²的值是．

查看试题解析

三、解答题

17. 合并同类项：

(1)、 $a + 4 b + 2 a - 3 b - a$ ；

(2)、 $\frac{1}{3} (3 a^{2} + b) - \frac{2}{3} (6 a^{2} - b)$ .

查看试题解析
18. 先化简下式，再求值： $- \frac{11}{2} x - 2 (x - \frac{1}{3} y^{2}) - 3 (- \frac{3}{2} x + \frac{1}{3} y^{2})$ ，其中 $x = - 2 ， y = - \frac{1}{3}$

查看试题解析
19. 三角形的周长为32，第一边长为3a+2b,第二边比第一边的2倍少a-2b,求第三边长.

查看试题解析
20. 小明同学准备化简：(2x²-3x-1)-(x²-2x□3)，算式中“□”是“+，-，×，÷中的某一种运算符号

(1)、若“□”是“×”，请你化简：(2x²-3x-1)-(x²-2x□3)

(2)、当x=1时，(2x²-3x-1)-(x²-2x□3)的结果是2，请你通过计算说明“□”所代表的运算符号

查看试题解析
21. 已知：有理数m所表示的点到表示3的点距离4个单位，a、b互为相反数，且都不为零，c、d互为倒数.

(1)、求m的值，

(2)、求： $2 a + 2 b + (\frac{a}{b} - 3 c d) - m$ 的值.

查看试题解析
22. 解答下列各题：

(1)、按由小到大的顺序排列五个连续整数，已知第二个整数是 $- 5$ ，求这五个连续整数的乘积；

(2)、三个连续奇数中，中间一个是 $2 n + 1$ ，求这三个连续奇数的和.

查看试题解析

23. 某市居民使用自来水按如下标准收费（水费按月缴纳）

户月用水量	单价
不超过12 m³的部分	2元/m³
超过12 m³但不超过20 m³的部分	3元/m³
超过20 m³的部分	4元/m³

(1)、某用户一个月用了14 m³水，求该用户这个月应缴纳的水费

(2)、某户月用水量为n立方米（12＜n≤20），该用户缴纳的水费是39元，列方程求n的值

(3)、甲、乙两用户一个月共用水40 m³ ，设甲用户用水量为x m³ ，且12＜x≤28

① 当12＜x≤20时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）

② 当20＜x≤28时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）

查看试题解析

24. 我们自从有了用字母表示数，发现表达有关的数和数量关系更加简洁明了，从而更助于我们发现更多有趣的结论，请你按要求试一试。

(1)、用代数式表示：
① $a$ 与 $b$ 的差的平方；② $a$ 、 $b$ 两数的平方和与 $a$ ， $b$ 两数积的2倍的差；

(2)、当 $a$ ＝3， $b$ ＝－2时，求第(1)题中①②所列的代数式的值；

(3)、由第(2)题的结果，你发现了什么等式？

(4)、利用你发现的结论：求2018²－2×2018×2017＋2017²的值．

查看试题解析

浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算 基础巩固

一、单选题

二、填空题

三、解答题

浙教版2019-2020学年初中数学七年级上学期期末复习专题3 代数式及其运算基础巩固