2017年江西省上饶市广丰区中考数学一模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
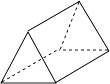
1. ﹣ 的绝对值是( )A、5 B、﹣5 C、 D、﹣2. 某网站数据显示,2015年第一季度我国彩电销量为1233万台,将1233万用科学记数法可表示为( )A、12.33×105 B、1.233×103 C、0.1233×108 D、1.233×1073. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 计算(x2)3÷(﹣x)2的结果是( )A、x2 B、x3 C、﹣x3 D、x45. 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
4. 计算(x2)3÷(﹣x)2的结果是( )A、x2 B、x3 C、﹣x3 D、x45. 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )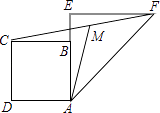 A、2 B、3 C、 D、6. 如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A、2 B、3 C、 D、6. 如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )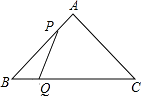 A、
A、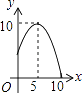 B、
B、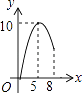 C、
C、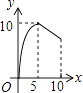 D、
D、
二、填空题
-
7. 因式分解:x3﹣4xy2= .8. 定义运算:x⊗y= ,则(﹣1)⊗2= .9. 关于x的一元二次方程mx2+(2m﹣1)x+m=0有两个不相等的实数根,则m的取值范围是 .10.
下列图形:它们是按一定规律排列的,依照此规律,第n个图形共有个★.
 11. 已知对任意锐角α、β均有:cos(α+β)=cosα•cosβ﹣sinα•sinβ,则cos75°= .12. 如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于 .
11. 已知对任意锐角α、β均有:cos(α+β)=cosα•cosβ﹣sinα•sinβ,则cos75°= .12. 如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于 .
三、解答题
-
13. 综合题。(1)、计算:(tan60°)﹣1× ﹣|﹣ |+23×0.125(2)、解方程:(x﹣5)2=16.14. 先化简,再求值:x(x﹣2)﹣(x+2)(x﹣2),其中x= .15. 关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2 .(1)、求k的取值范围;(2)、如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.16. 应用无刻度的直尺画图:

在下面的三个图中,以OA为边,在正方形网格内作∠AOB=α,B点为格点(每个小正方形的顶点)使sinα的值分别为: , 和 .
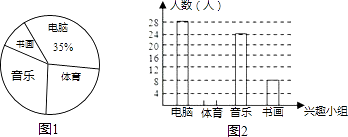
17. 在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其他都相同,(1)、在其中一个口袋中一次性随机摸出两个球,请写出在这一过程中的一个必然事件;(2)、若分别从两个袋中随机取出一个球,试求出两个小球颜色相同的概率.18. 如图,一次函数 的图象分别交x轴、y轴于A,B两点,且与反比例函数 (x>0)的图象在第一象限交于点C(4,n),CD⊥x轴于D.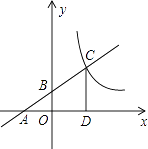 (1)、求m,n的值;(2)、求△ADC的面积.19. 实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
(1)、求m,n的值;(2)、求△ADC的面积.19. 实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:请你根据统计图1、2中提供的信息,
解答下列问题:
(1)、写出2条有价值信息(不包括下面要计算的信息);(2)、这次抽样调查的样本容量是多少?在图2中,请将小易画的统计图中的“体育”部分的图形补充完整;(3)、爱好“书画”的人数占被调查人数的百分数是多少?估计实验中学现有的学生中,有多少人爱好“书画”?20. 如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm. (1)、当PA=45cm时,求PC的长;(2)、若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ≈1.414, ≈1.732)21. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)、当PA=45cm时,求PC的长;(2)、若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ≈1.414, ≈1.732)21. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.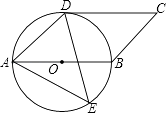 (1)、试判断CD与⊙O的位置关系,并证明你的结论;(2)、若⊙O的半径为3,sin∠ADE= ,求AE的值.22. 如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
(1)、试判断CD与⊙O的位置关系,并证明你的结论;(2)、若⊙O的半径为3,sin∠ADE= ,求AE的值.22. 如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.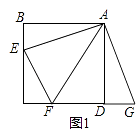
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
(1)、如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明; (2)、如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
(2)、如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.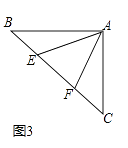 23. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
23. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t. (1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
(1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.