浙教版2019-2020学年初中数学七年级上学期期末复习专题1 实数的认识 提高训练

试卷更新日期：2019-12-12 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 下面说法正确的是（   ）
    A、相反数和本身相等的数是不存在的 B、数轴上原点两侧的两个点所表示的数互为相反数 C、数轴上的一个点只能表示一个数 D、若一个数是有理数，则这个数一定是分数

    查看试题解析

  • 2. 下列说法正确的是（ ）
    A、一个正数的平方根和立方根都只有一个； B、0 的平方根和立方根都是0； C、1 的平方根与立方根都等于它本身； D、一个数的立方根与其自身相等的数只有-1

    查看试题解析

  • 3. 实 数 1−2a 有平方根，则 a 可以取的值为 （ ）
    A、12 B、1 C、2 D、π

    查看试题解析

  • 4. 若 |x−1|+|y+3|=0 ，那么 (x+1)(y−3) 等于（   ）
    A、0 B、-3 C、-6 D、-12

    查看试题解析

  • 5. 学完有理数后，四只“羊”分别聊了起来.喜羊羊说：“没有最大的正数，但有最大的负数.” 懒羊羊说：“有绝对值最小的数，没有绝对值最大的数.” 美羊羊说：“有理数分为正有理数和负有 理数.” 沸羊羊说：“相 反数是它本身的数是正数.” 你认为哪只“羊”说得对呢？（    ）
    A、喜羊羊 B、懒羊羊 C、美羊羊 D、沸羊羊

    查看试题解析

  • 6. 学校、家、书店座落在一条南北走向的大街上，学校在家南边20米，书店在家北边10米，张明从家里出发，向北走了50米，又向南走了70米，此时张明的位置在 （ ）
    A、在家 B、在学校 C、在书店 D、不在上述地方

    查看试题解析

  • 7. 某种零件，标明要求是φ20 -0.05+0.02 （φ表示直径，单位：毫米），则以下零件的直径合格的是（    ）
    A、19.50mm B、20.2mm C、19.95mm D、20.05mm

    查看试题解析

  • 8. 已知 abc>0 ，则式子： |a|a+|b|b+|c|c= （   ）
    A、3   B、−3 或1   C、−1 或3   D、1

    查看试题解析

  • 9. 如图1所示的是嘉淇爸爸给嘉淇出的一道题，如图2所示的是嘉淇对该题的解答.她所写的结论中，正确的个数是（   ）

    A、6 B、5 C、4 D、3

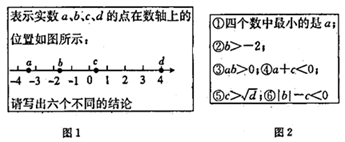    查看试题解析

  • 10. 已知 min{x ， x2 ， x} 表示取三个数中最小的那个数﹒例如：当 x=9 ， min{x ， x2 ， x} = min{9 ， 92 ， 9} =3﹒当 min{x ， x2 ， x} = 116 时，则 x 的值为（   ）
    A、116 B、18 C、14 D、12

    查看试题解析

二、填空题

  • 11. 如图所示，M，N，P，R分别是数轴上的四个整数所对应的点，其中有一个点是原点，并且，MN=NP=PR=1，数a对应的点在M和N之间，数b对应的点在P和R之间，若|a|+|b|=2， 则原点是（填M，N，P，R中的一个或几个）.


    查看试题解析

  • 12. A是数轴上的一点，将点A沿数轴移动3个单位长度至点B，再将点B沿数轴移动4个单位长度至点C，若点C表示原点，用字母a、b分别表示点A、B在数轴上所对应的数，则|a＋b|的值为。

    查看试题解析

  • 13. 有三个数 a ， b ， c ，其中 a 没有平方根， b>b,c<c ，则这三个数按照从小到大的顺序排列应为： < < ．

    查看试题解析

  • 14. 根据如图所示的计算程序，若输入的 x 的值为 16 的算术平方根，则输出的 y 的值为.

    查看试题解析

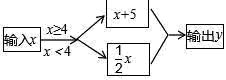  • 15. 如果x、y都是不为0的有理数，则代数式 x|x|+|y|y−xy|xy| 的最大值是.

    查看试题解析

  • 16. (2+1)(2−1)=1,(3+2)(3−2)=1,(4+3)(4−3)=1,(5+4)(5−4)=1...... 利用上面的规律，比较 11−10 12−11 的大小.（填“>”或“<”）.

    查看试题解析

三、解答题

  • 17. 已知数轴上有A，B两点，A，B两点间的距离为2，点B到原点O的距离为4，求所有满足条件的点A所表示的数，并求出这些点到原点O的距离之和．

    查看试题解析

  • 18. 已知某种零件的标准直径是10mm，超出规定直径长度的数量（mm）记作正数，不足规定直径长度的数量（mm）记作负数，检验员某次抽查了五件样品，检查的结果如下:

    序号

    1

    2

    3

    4

    5

    直径长度/mm

    +0.1

    -0.15

    0.2

    -0.05

    +0.25
    (1)、试指出哪件样品的大小最符合要求？
    (2)、如果规定误差的绝对值在0.18mm之内的是合格品，误差的绝对值在0.18mm~0.22mm之间是次品，误差的绝对值超过0.22mm的是废品，那么上述五件样品中，哪些是合格品，哪些是次品，哪些是废品？

    查看试题解析

  • 19. 操作探究：已知在纸面上有一数轴（如图所示），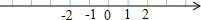

    操作一：

    ⑴折叠纸面，使表示的1点与-1表示的点重合，则-3表示的点与  ▲  表示的点重合；

    操作二：

    ⑵折叠纸面，使-1表示的点与3表示的点重合，回答以下问题：

    ①5表示的点与数  ▲  表示的点重合；

    ②若数轴上A、B两点之间距离为11，（A在B的左侧），且A、B两点经折叠后重合，求A、B两点表示的数是多少．

    查看试题解析

  • 20. 如图，一只甲虫在 5×5 的方格（每小格边长为 1）上沿着网格线运动.它从 A处出发去看望 B、C、D 处的其它甲虫，规定：向上向右走为正，向下向左走为负.如果从 A 到 B 记为：A→B（+1，+4），从 B 到 A 记为：B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中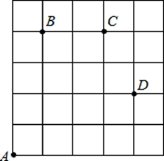

    (1)、A→C（ ， ），B→C（ ， ），C→D  （ ， ）；
    (2)、若这只甲虫的行走路线为 A→B→C→D ， 请计算该甲虫走过的最少路程；
    (3)、若这只甲虫从 A 处去甲虫 P 处的行走路线依次为（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），请在图中标出P 的位置.

    查看试题解析

  • 21.     
    (1)、如图，有一根木棒MN放置在数轴上，它的两端M、N分别落在点A、B．将木棒在数轴上水平移动，当点M移动到点B时，点N所对应的数为20，当点N移动到点A时，点M所对应的数为5．（单位：cm）则木棒MN长为cm．

    (2)、一天，小民去问爷爷的年龄，爷爷说：“我若是你现在这么大，你还要40年才出生呢，你若是我现在这么大，我已经是老寿星了，125岁了，哈哈！”请你借助上述方法，写出小民爷爷到底是岁.

    查看试题解析

  • 22. 阅读下面的文字，解答问题

    大家知道， 2 是无理数，而无理数是无限不循环小数，因此 2 的小数部分我们不可能全部地写出来，于是小明用 2 ﹣1来表示 2 的小数部分，你同意小明的表示方法吗？

    事实上，小明的表示方法是有道理的，因为 2 的整数部分是1，将这个数减去其整数部分，差就是小数部分．

    又例如因为 4 ＜ 7 ＜ 9 ，即2＜ 7 ＜3，所以行的整数部分为2，小数部分为 7 ﹣2．

    请解答

    (1)、83 的整数部分为；小数部分为；
    (2)、有人说，如果 83 的整数部分为x， 97 的小数部分记为y，则x+y= 97 ，你认为对吗？为什么？
    (3)、如果 35 的整数部分为a， 35 的小数部分为b，求a﹣2b+2 35 的值．

    查看试题解析

  • 23. 同学们，我们都知道：|5-2|表示5与2的差的绝对值，实际上也可理解为5与2两数在数轴上所对应的两点之间的距离；|5+2|表示5与-2的差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离，试探索：
    (1)、|﹣4+6|=；|﹣2﹣4|=；
    (2)、找出所有符合条件的整数x，使|x+2|+|x-1|=3成立；
    (3)、若数轴上表示数a的点位于﹣4与6之间，求|a+4|+|a﹣6|的值；
    (4)、当a=时，|a﹣1|+|a+5|+|a﹣4|的值最小，最小值是；
    (5)、当a=时，|a﹣1|+|a+2|+|a﹣3|+|a+4|+|a﹣5|+…+|a+2n|+|a﹣(2n+1)|的值最小，最小值是.

    查看试题解析