2017年江西省萍乡市中考数学二模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
1. 1不是﹣1的( )A、 相反数 B、绝对值 C、平方数 D、倒数2. 下列等式一定成立的是( )A、a2+a2=a5 B、(a﹣1)2=a2﹣1 C、(﹣a)9÷(﹣a)3=a6 D、(﹣2a2)3=8a63. 如图是由四个小正方体叠成的一个立体图形,那么它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、
4. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、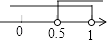 D、
D、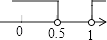 5.
5.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
 A、
A、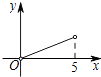 B、
B、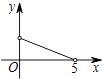 C、
C、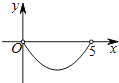 D、
D、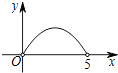 6. 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( )
6. 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( ) A、9 B、6 C、3 D、3
A、9 B、6 C、3 D、3二、填空题
-
7. 若△ABC∽△DEF,相似比为2:3,则S△ABC:S△DEF= .8. 计算(﹣ )﹣1+(2 ﹣1)0﹣|tan45°﹣2 |= .9. 餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,500亿用科学记数法表示为 .10. 如图,AB、AC是⊙O的两条弦∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数是 .
 11. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b= .
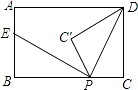
11. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b= . 12. 如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF= .
12. 如图,在矩形ABCD中,AB=4,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在直线EB′与AD的交点C′处,DF= .
三、解答题
-
13. 解方程:3x(x﹣2)=2(2﹣x);14. 如图,PA,PB分别与⊙O相切于点A,B,连接AB,∠APB=60°,AB=5,求PA的长.
 15. 化简求值: ÷( ﹣a),其中a= ﹣2.16. 某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?17. 体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
15. 化简求值: ÷( ﹣a),其中a= ﹣2.16. 某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?17. 体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. (1)、补全频数分布直方图;(2)、扇形图中m=;(3)、若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?18. 请仅用无刻度的直尺在下列图1和图2中按要求画菱形.
(1)、补全频数分布直方图;(2)、扇形图中m=;(3)、若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?18. 请仅用无刻度的直尺在下列图1和图2中按要求画菱形. (1)、图1是矩形ABCD,E,F分别是AB和AD的中点,以EF为边画一个菱形;(2)、图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.19. 甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表)
(1)、图1是矩形ABCD,E,F分别是AB和AD的中点,以EF为边画一个菱形;(2)、图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形.19. 甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表)甲超市:
球
两红
一红一白
两白
礼金券(元)
5
10
5
乙超市:
球
两红
一红一白
两白
礼金券(元)
10
5
10
(1)、用树状图表示得到一次摸奖机会时中礼金券的所有情况;(2)、如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.20. 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ≈1.414, ≈1.732,最后结果精确到1米). 21. 在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y= 交于点B(m,2)
21. 在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y= 交于点B(m,2) (1)、求点B的坐标及k的值;(2)、将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式.22. 在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)、如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(1)、求点B的坐标及k的值;(2)、将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式.22. 在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)、如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD. (2)、如图2,AC:AB=1: ,EF⊥CE,求EF:EG的值.
(2)、如图2,AC:AB=1: ,EF⊥CE,求EF:EG的值. 23. 如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
23. 如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. (1)、线段AE=;(2)、如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
(1)、线段AE=;(2)、如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.

①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= 时,DM与⊙O相切.
四、解答题
-
24.
如图1(注:与图2完全相同),二次函数y= x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
 (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).