2017年江苏省扬州市宝应县中考数学二模试卷

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的倒数是（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 下列各算式中，合并同类项正确的是（）

A、x²+x²=2x² B、x²+x²=x⁴ C、2x²﹣x²=2 D、2x²﹣x²=2x

查看试题解析
3. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{9}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
4. 高速路上因赶时间超速而频频发生交通事故，这样给自己和他人的生命安全带来直接影响，为了解车速情况，一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下：
车序号
1
2
3
4
5
6
车速（千米/时）
100
95
106
100
120
100
则这6辆车车速的众数和中位数（单位：千米/时）分别是（）

A、100，95 B、100，100 C、102，100 D、100，103

查看试题解析
5. 若点A（﹣1，2），B（2，﹣3）在直线y=kx+b上，则函数y= $\frac{k}{x}$ 的图象在（）

A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第二、三象限

查看试题解析
6. 如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于点E，则sin∠E的值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E，F同时由A，C两点出发，分别沿AB，CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为（）

A、1 B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{4}{3}$

查看试题解析
8. 如图，⊙O是以原点为圆心，2 $\sqrt{3}$ 为半径的圆，点P是直线上y=﹣x+8的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（）

A、4 B、2 $\sqrt{5}$ C、8﹣2 $\sqrt{3}$ D、2 $\sqrt{13}$

查看试题解析

二、填空题

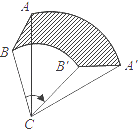
9. 因式分解：m²﹣4n²= ．

查看试题解析
10. 4月26日在国务院新闻办公室新闻发布会上，工业和信息化部发布的信息显示，我国4G用户增速持续攀升，一季度末总数达到8.36亿户，将8.36亿用科学记数法表示为．

查看试题解析
11. 在函数y= $\frac{2017}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 一次函数y=kx+b与正比例函数y=3x的图象平行且经过点（1，﹣1），则b的值为．

查看试题解析
13. 如图，将△ABC绕点C旋转60°得到△A′B′C′，已知AC=6，BC=4，则线段AB扫过图形（阴影部分）的面积为．（结果保留π）

查看试题解析
14. 如图，直线l₁∥l₂∥l₃ ，等边△ABC的顶点B、C分别在直线l₂、l₃上，若边BC与直线l₃的夹角∠1=25°，则边AB与直线l₁的夹角∠2= ．

查看试题解析
15. 若关于x的一元二次方程x²﹣2x﹣k=0没有实数根，则k的取值范围是

查看试题解析
16. 如图，二次函数y₁=ax²+bx+c与一次函数y₂=kx的图象交于点A和原点O，点A的横坐标为﹣4，点A和点B关于抛物线的对称轴对称，点B的横坐标为1，则满足0＜y₁＜y₂的x的取值范围是．

查看试题解析
17. 如图，ABCD是⊙O的内接四边形，点E在AB的延长线上，BF是∠CBE的平分线，∠ADC=110°，则∠FBE= ．

查看试题解析
18. 如图，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是 $\hat{A B}$ 上一点．将扇形AOB沿EF对折，使得折叠后的圆弧 $\hat{A' F}$ 恰好与半径OB相切于点G．若OE=4，则O到折痕EF的距离为．

查看试题解析

三、解答题

19. 计算：2tan60°﹣（ $\frac{1}{3}$ ）^﹣¹+（﹣2）²×（2017﹣sin45°）⁰﹣|﹣ $\sqrt{12}$ |

查看试题解析
20. 先化简，后求值： $(\frac{3 x}{x - 1} - \frac{x}{x + 1}) \cdot \frac{x^{2} - 1}{x}$ ，其中x=﹣2．

查看试题解析
21.
如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形，建立如图所示的平面直角坐标系，点C的坐标为（0，﹣1）．

(1)、在如图的方格纸中把△ABC以点O为位似中心扩大，使放大前后的位似比为1：2，画出△A₁B₂C₂（△ABC与△A₁B₂C₂在位似中心O点的两侧，A，B，C的对应点分别是A₁ ， B₂ ， C₂）．

(2)、利用方格纸标出△A₁B₂C₂外接圆的圆心P，P点坐标是⊙P的半径= ．（保留根号）

查看试题解析
22.
为贯彻落实习近平总书记关于弘扬中华优秀传统文化的指示精神，进一步发挥“中国汉字听写大会”和“中国诗词大会”在传承弘扬优秀传统文化中的品牌辐射作用，提升我市中学生的传统文化素养，为参加省赛、国赛做好准备，2017年拟继续举办扬州市中学生汉字听写、诗词诵写大赛．宝应县和高邮市经过初赛、复赛，各选出5名选手组成宝应代表队和高邮代表队参加市7月份的决赛．两个队各选出的5名选手的复赛成绩如图所示．

(1)、根据图示填写下表；

平均数（分）
中位数（分）
众数（分）
宝应
83
85
高邮
95

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．

查看试题解析
23. 小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．

(1)、如果小明第一题不使用“求助”，那么小明答对第一道题的概率是．

(2)、如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．

(3)、从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）

查看试题解析
24. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．

(1)、证明：四边形ACDE是平行四边形；

(2)、若AC=8，BD=6，求△ADE的周长．

查看试题解析
25. 如图，一种拉杆式旅行箱的示意图，箱体长AB=50cm，拉杆最大伸长距离BC=30cm，（点A、B、C在同一条直线上），在箱体的底端装有一圆形滚轮⊙A，其直径为10cm，⊙A与水平地面切于点D，过A作AE∥DM．当人的手自然下垂拉旅行箱时，人感觉较为舒服，已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时，点C距离水平地面（40 $\sqrt{3}$ +5）cm，求此时拉杆箱与水平面AE所成角∠CAE的大小及点B到水平地面的距离．

查看试题解析
26. 水果店张阿姨以每斤4元的价格购进某种水果若干斤，然后以每斤6元的价格出售，每天可售出150斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出30斤，为保证每天至少售出360斤，张阿姨决定降价销售．

(1)、若将这种水果每斤的售价降低x元，则每天的销售量是斤（用含x的代数式表示）；

(2)、销售这种水果要想每天盈利450元，张阿姨需将每斤的售价降低多少元？

查看试题解析
27. 在平面直角坐标系中，矩形OABC的边OA、OC分别落在x轴、y轴上，O为坐标原点，且OA=8，OC=4，连接AC，将矩形OABC对折，使点A与点C重合，折痕ED与BC交于点D，交OA于点E，连接AD，如图①．

(1)、求点D的坐标和AD所在直线的函数关系式；

(2)、⊙M的圆心M始终在直线AC上（点A除外），且⊙M始终与x轴相切，如图②．
①求证：⊙M与直线AD相切；
②圆心M在直线AC上运动，在运动过程中，能否与y轴也相切？如果能相切，求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标；如果不能相切，请说明理由．

查看试题解析
28.
如图，已知抛物线 $y = - \frac{1}{3} x^{2} + \frac{2}{3} x + 5$ 与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，有一宽度为1的刻度尺沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线AC于点M和点N，交x轴于点E和点F．

(1)、求点A、B、C的坐标；

(2)、当点M和点N都在线段AC上时，连接EN，如果点E的坐标为（4，0），求sin∠ANE的值；

(3)、在刻度尺平移过程中，当以点P、Q、N、M为顶点的四边形是平行四边形时，求点N的坐标．

查看试题解析

	平均数（分）	中位数（分）	众数（分）
宝应	83	85
高邮			95

车序号	1	2	3	4	5	6
车速（千米/时）	100	95	106	100	120	100