2017年江苏省盐城市阜宁县中考数学二模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
1. 下列各数中,最大的是( )A、0 B、1 C、﹣1 D、﹣2. 下列事件中是必然事件的是( )A、明天太阳从西边升起 B、篮球队员在罚球线上投篮一次,未投中 C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面朝上3. 下列几何体的主视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、x+x2=x3 B、2x+3x=5x C、(x2)3=x5 D、x6÷x3=x25. 如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )
4. 下列计算正确的是( )A、x+x2=x3 B、2x+3x=5x C、(x2)3=x5 D、x6÷x3=x25. 如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )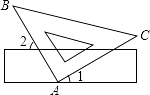 A、60° B、50° C、40° D、30°6. 下列四个命题:
A、60° B、50° C、40° D、30°6. 下列四个命题:⑴数据5、2、﹣3、0的极差是8;
⑵方差越大,说明数据就越稳定;
⑶不在同一直线上的三点确定一个圆;
⑷在半径为5的⊙O中,弦AB∥CD,且AB=6,CD=8,则AB与CD之间距离为7
其中真命题的个数为( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
7. 计算:|﹣ |= .8. 函数y= 中,自变量x的取值范围是 .9. 在平面直角坐标系中,已知一次函数y=3﹣2x的图象经过P1(x1 , y1),P2(x2 , y2)两点,若x1<x2 , 则y1y2 . (填“>”,“<”或“=”)10. 规定用符号[x]表示一个实数的整数部分,例如[289]=2,[ ]=1,按此规定,[ ﹣1]= .11.
如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面相对面上的字是 .
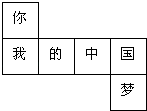 12. 如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,测得MN=39m,则A,B两点间的距离是 m.
12. 如图,为估计池塘两岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,测得MN=39m,则A,B两点间的距离是 m. 13. 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= .
13. 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= . 14. 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=度.
14. 如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,连接AD若∠A=28°,则∠C=度. 15. 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
15. 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y= 的图象上,OA=2,OC=6,则正方形ADEF的边长为 . 16. 如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .
16. 如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .
三、解答题
-
17. 计算: ﹣4cos60°+(2017﹣π)0﹣32 .18. 先化简再求值:(x+2﹣ )÷( + ),其中x是不等式组 的整数解.19.
为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
 (1)、本次接受随机抽样调查的学生人数为 , 图①中m的值为;(2)、求本次调查获取的样本数据的众数和中位数;(3)、根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?20.
(1)、本次接受随机抽样调查的学生人数为 , 图①中m的值为;(2)、求本次调查获取的样本数据的众数和中位数;(3)、根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?20.方格纸中每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.

①在10×10的方格中(每个小方格的边长为1个单位),画一个面积为2的格点钝角三角形ABC,并标明相应字母;
②再在方格中画一个格点△DEF,使得△DEF∽△ABC,且面积之比为2:1,并加以证明.
21. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.(1)、请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;(2)、规定当两次摸出的小球标号相同时中奖,求中奖的概率.22. 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC. (1)、求被剪掉阴影部分的面积;(2)、用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?23. 县内某小区正在紧张建设中,现有大量的沙石需要运输,“建安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)、求“建安”车队载重量为8吨、10吨的卡车各有多少辆?(2)、随着工程的进展,“建安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.24.
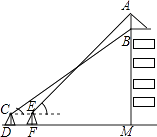
(1)、求被剪掉阴影部分的面积;(2)、用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?23. 县内某小区正在紧张建设中,现有大量的沙石需要运输,“建安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)、求“建安”车队载重量为8吨、10吨的卡车各有多少辆?(2)、随着工程的进展,“建安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.24.我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: ≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
 25. 已知:抛物线C1: 与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.(1)、求m,n的值;(2)、试写出x为何值时,y1>y2?(3)、试描述抛物线C1通过怎样的变换得到抛物线C2 .26.
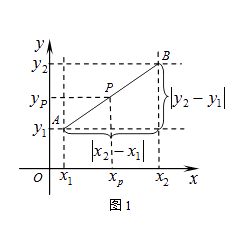
25. 已知:抛物线C1: 与C2:y=x2+2mx+n具有下列特征:①都与x轴有交点;②与y轴相交于同一点.(1)、求m,n的值;(2)、试写出x为何值时,y1>y2?(3)、试描述抛物线C1通过怎样的变换得到抛物线C2 .26.阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),AB中点P的坐标为(xp , yp).由xp﹣x1=x2﹣xp , 得xp= ,同理yp= ,所以AB的中点坐标为( , ).由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A、B两点间的距离公式为AB= .这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
 (1)、已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .(2)、
(1)、已知M(1,﹣2),N(﹣1,2),直接利用公式填空:MN中点坐标为 , MN= .(2)、如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
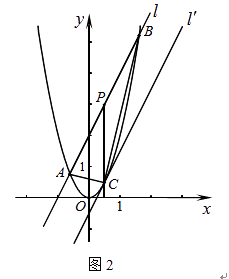
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
27.图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ,A(3,0),D(﹣1,0),E(0,3).
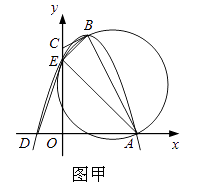
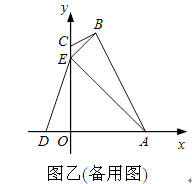 (1)、求抛物线的解析式及顶点B的坐标;(2)、求证:CB是△ABE外接圆的切线;(3)、试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及顶点B的坐标;(2)、求证:CB是△ABE外接圆的切线;(3)、试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由.