2017年江苏省盐城市滨海县联盟校中考数学二模试卷
试卷更新日期:2017-07-25 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数是( )A、 B、﹣3 C、3 D、﹣2. 下列四个数中,无理数是( )A、 B、 C、0 D、|﹣5|3. 下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 如图所示,该几何体的俯视图是( )
4. 如图所示,该几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
5. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、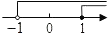 B、
B、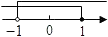 C、
C、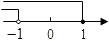 D、
D、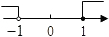 6. 下列图形中,∠2>∠1的是( )A、
6. 下列图形中,∠2>∠1的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. |a|=(2017)0 , 则a= .8. 当x=时,分式 的值为0.9. 计算: + = .10. 某舞蹈队10名队员的年龄分布如下表所示:
年龄(岁)
13
14
15
16
人数
2
5
2
1
则这10名队员年龄的众数是 .
11. 小明把如图所示的平行四边形纸板挂在墙上,完飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是 . 12. 如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B=°.
12. 如图,在直角三角形ABC中,斜边AB上的中线CD=AC,则∠B=°. 13. 线段AB的长为5,点A在平面直角坐标系中的坐标为(3,2),点B的坐标为(x,2),则点B的坐标为 .14.
13. 线段AB的长为5,点A在平面直角坐标系中的坐标为(3,2),点B的坐标为(x,2),则点B的坐标为 .14.找出下列各图形中数的规律,以此类推,a的值为 .
 15. 如图,四边形ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=100°,则∠FBE=°.
15. 如图,四边形ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=100°,则∠FBE=°. 16. 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为 .
16. 在△ABC中,点D、E分别在AB、AC上,且CD于BE相交于点F,已知△BDF的面积为12,△BCF的面积为16,△CEF的面积为12,则四边形ADFE的面积为 .
三、解答题
-
17. ﹣ +|﹣3|.18. 设a,b是方程x2+2x﹣2019=0的两个不相等的实数根.(1)、a+b=;ab=;2a2+4a=;(2)、求代数式a2+3a+b的值.19. 若关于x,y的二元一次方程组 的解满足x+y>﹣ .
求出满足条件的所有正整数m的值.
20. 在一个不透明的袋子中装有白色、黄色和蓝色三种颜色的小球,这些球除颜色外都相同,其中白球有2个,蓝球有1个.现从中任意摸出一个小球是白球的概率是 .(1)、袋子中黄色小球有个;(2)、如果第一次任意摸出一个小球(不放回),第二次再摸出一个小球,请用画树状图或列表格的方法求两次都摸出白球的概率.21. 为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A,B,C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整),请你结合图中的信息,解答下列问题: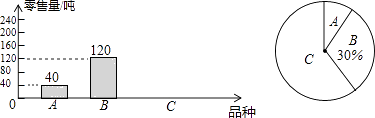 (1)、该市场6月上半月共销售这三种荔枝多少吨?(2)、补全图1的统计图并计算图2中A所在扇形的圆心角的度数;(3)、某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?22. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点.
(1)、该市场6月上半月共销售这三种荔枝多少吨?(2)、补全图1的统计图并计算图2中A所在扇形的圆心角的度数;(3)、某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?22. 如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点. (1)、求反比例函数的表达式;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;(3)、求△PAB的面积.23. 如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= .
(1)、求反比例函数的表达式;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;(3)、求△PAB的面积.23. 如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= . (1)、求旗杆EF的高(结果保留根号);(2)、求旗杆EF与实验楼CD之间的水平距离DF的长.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F.
(1)、求旗杆EF的高(结果保留根号);(2)、求旗杆EF与实验楼CD之间的水平距离DF的长.24. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F. (1)、求证:OE=CD;(2)、若菱形ABCD的边长为4,∠ABC=60°,求AE的长.25. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
(1)、求证:OE=CD;(2)、若菱形ABCD的边长为4,∠ABC=60°,求AE的长.25. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. (1)、用尺规补全图形(保留作图痕迹,不写作法);(2)、求证:BC与⊙O相切;(3)、当AD= ,∠CAD=30°时,求劣弧AD的长.26. 如图,抛物线y= x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣ ).直线y=mx+ 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
(1)、用尺规补全图形(保留作图痕迹,不写作法);(2)、求证:BC与⊙O相切;(3)、当AD= ,∠CAD=30°时,求劣弧AD的长.26. 如图,抛物线y= x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣ ).直线y=mx+ 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M. (1)、求抛物线y= x2+bx+c的表达式及点D的坐标;(2)、若四边形PEMN是平行四边形?请求出点P的坐标;(3)、过点P作PF⊥BD于点F,设△PEF的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.27. 如图1,在矩形ABCD中,AB=8,BC=6,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)、求抛物线y= x2+bx+c的表达式及点D的坐标;(2)、若四边形PEMN是平行四边形?请求出点P的坐标;(3)、过点P作PF⊥BD于点F,设△PEF的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.27. 如图1,在矩形ABCD中,AB=8,BC=6,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒). (1)、如图2,当点N落在BD上时,求t的值;
(1)、如图2,当点N落在BD上时,求t的值; (2)、当正方形PQMN的边经过点O时(包括正方形PQMN的顶点),求此时t的值;(3)、当点P在边AD上运动时,求S与t之间的函数关系式;(4)、写出在点P运动过程中,直线DN恰好平分△BCD面积时t的所有可能值.
(2)、当正方形PQMN的边经过点O时(包括正方形PQMN的顶点),求此时t的值;(3)、当点P在边AD上运动时,求S与t之间的函数关系式;(4)、写出在点P运动过程中,直线DN恰好平分△BCD面积时t的所有可能值.