人教新课标A版必修1数学2.2.2 对数函数及其性质同步测试
试卷更新日期:2017-07-25 类型:同步测试
一、单选题
-
1. 函数y= 的定义域是( )A、(1,2] B、(1,2) C、(2,+∞) D、(﹣∞,2)2. 函数 的定义域是( )A、[1,2] B、[1,2) C、 D、3. 已知函数f(x)=|lgx|.若a≠b且,f(a)=f(b),则a+b的取值范围是( )A、(1,+∞) B、[1,+∞) C、(2,+∞) D、[2,+∞)4. 设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为 , 则实数a的值为( )A、 B、 C、 D、5. 函数y= 的图象大致是( )A、
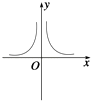 B、
B、 C、
C、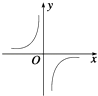 D、
D、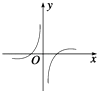 6. 下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是( )A、y=x B、y=lgx C、y=2x D、y=7. 已知函数f(x)=ax+logax(a>0且a≠1)在[1,2]上的最大值与最小值之和为(loga2)+6,则a的值为( )A、 B、 C、2 D、48. 为了得到函数y=lg 的图象,只需把函数y=lg x的图象上所有的点( )A、向左平移3个单位长度,再向上平移1个单位长度 B、向右平移3个单位长度,再向上平移1个单位长度 C、向左平移3个单位长度,再向下平移1个单位长度 D、向右平移3个单位长度,再向下平移1个单位长度9. 函数y=ax与y=﹣logax(a>0,且a≠1)在同一坐标系中的图象只可能是( )A、
6. 下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是( )A、y=x B、y=lgx C、y=2x D、y=7. 已知函数f(x)=ax+logax(a>0且a≠1)在[1,2]上的最大值与最小值之和为(loga2)+6,则a的值为( )A、 B、 C、2 D、48. 为了得到函数y=lg 的图象,只需把函数y=lg x的图象上所有的点( )A、向左平移3个单位长度,再向上平移1个单位长度 B、向右平移3个单位长度,再向上平移1个单位长度 C、向左平移3个单位长度,再向下平移1个单位长度 D、向右平移3个单位长度,再向下平移1个单位长度9. 函数y=ax与y=﹣logax(a>0,且a≠1)在同一坐标系中的图象只可能是( )A、 B、
B、 C、
C、 D、
D、 10. 设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为 ,则a=( )A、 B、2 C、2 D、411. 若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )A、0<a<1 B、0<a<2,a≠1 C、1<a<2 D、a≥212. 已知函数f(x)=logsin1(x2﹣ax+3a)在[2,+∞)单调递减,则实数a的取值范围是( )A、(﹣∞,4] B、[4,+∞) C、[﹣4,4] D、(﹣4,4]13. 已知e是自然对数的底数,函数f(x)=ex+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式中成立的是( )A、f(a)<f(1)<f(b) B、f(a)<f(b)<f(1) C、f(1)<f(a)<f(b) D、f(b)<f(1)<f(a)
10. 设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为 ,则a=( )A、 B、2 C、2 D、411. 若函数y=loga(x2﹣ax+1)有最小值,则a的取值范围是( )A、0<a<1 B、0<a<2,a≠1 C、1<a<2 D、a≥212. 已知函数f(x)=logsin1(x2﹣ax+3a)在[2,+∞)单调递减,则实数a的取值范围是( )A、(﹣∞,4] B、[4,+∞) C、[﹣4,4] D、(﹣4,4]13. 已知e是自然对数的底数,函数f(x)=ex+x﹣2的零点为a,函数g(x)=lnx+x﹣2的零点为b,则下列不等式中成立的是( )A、f(a)<f(1)<f(b) B、f(a)<f(b)<f(1) C、f(1)<f(a)<f(b) D、f(b)<f(1)<f(a)二、填空题
-
14. 已知 , ,c=log32.则a,b,c的大小关系为: .15. 函数y=loga(3x﹣7)+1的图象恒过定点 .16. 已知f(x)= 是(﹣∞,+∞)上的减函数,那么a的取值范围是 .17. 若函数f(x)=loga(2x2+x)(a>0,a≠1)在区间恒有f(x)>0,则f(x)的单调递增区间是18. 若函数f(x)=loga(x﹣1)+4(a>0且a≠1)的图象过定点(m,n),则logmn=
三、解答题
-
19. 已知函数f(x)=lg[(m2﹣3m+2)x2+2(m﹣1)x+5],如果函数f(x)的值域为R,求实数m的取值范围.20. 求函数y=loga(x﹣x2)(a>0,a≠1)的单调区间及值域.
