2017年江苏省苏州市昆山市中考数学二模试卷

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题：

1. $\sqrt{3}$ 的相反数是（）

A、3 B、﹣3 C、 $\sqrt{3}$ D、﹣ $\sqrt{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 4)}^{2}}$ =﹣4 B、（a²）³=a⁵ C、a•a³=a⁴ D、2a﹣a=2

查看试题解析
3. 南海资源丰富，其面积约为350万平方千米，相当于我国的渤海、黄海和东海总面积的3倍．其中350万用科学记数法表示为（）

A、0.35×10⁸ B、3.5×10⁷ C、3.5×10⁶ D、35×10⁵

查看试题解析
4. 函数y= $\sqrt{2 x - 4}$ 中自变量x的取值范围是（）

A、x≥2 B、x＞2 C、x≤2 D、x≠2

查看试题解析
5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（）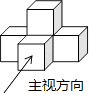

A、 B、 C、 D、

查看试题解析
7. 下列说法中，你认为正确的是（　　）

A、四边形具有稳定性 B、等边三角形是中心对称图形 C、等腰梯形的对角线一定互相垂直 D、任意多边形的外角和是360°

查看试题解析
8.
如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）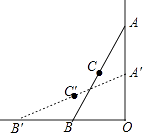

A、直线的一部分 B、圆的一部分 C、双曲线的一部分 D、抛物线的一部分

查看试题解析
9. 如图，在半径为 $\sqrt{5}$ 的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=4，则OP的长为（）

A、1 B、 $\sqrt{2}$ C、2 D、2 $\sqrt{2}$

查看试题解析
10.
如图，A、B、C是反比例函数y= $\frac{k}{x}$ （k＜0）图象上三点，作直线l，使A、B、C到直线l的距离之比为3：1：1，则满足条件的直线l共有（）

A、4条 B、3条 C、2条 D、1条

查看试题解析

二、填空题：

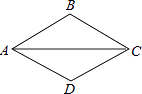
11. 因式分解：a²﹣2a= ．

查看试题解析
12. 掷一枚质地均匀的正方体骰子（六个面上分别刻有1到6的点数），向上一面出现的点数大于2且小于5的概率为．

查看试题解析
13. 已知x=﹣1是一元二次方程ax²+bx﹣10=0的一个解，且a≠﹣b，则 $\frac{a^{2} - b^{2}}{2 a + 2 b}$ 的值为．

查看试题解析
14. 如图，菱形ABCD的边长为15，sin∠BAC= $\frac{3}{5}$ ，则对角线AC的长为．

查看试题解析
15. 如图所示，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的直径是 cm．

查看试题解析
16. 已知二次函数y=ax²+bx+c（a≠0）中，函数值y与自变量x的部分对应值如下表：
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
…
y
…
3
﹣2
﹣5
﹣6
﹣5
…
则关于x的一元二次方程ax²+bx+c=﹣2的根是．

查看试题解析
17.
如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于．

查看试题解析
18. 赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，若这四个全等直角三角形的两条直角边分别平行于x轴和y轴，大正方形的顶点B₁、C₁、C₂、C₃、…、C_n在直线y=﹣ $\frac{1}{2}$ x+ $\frac{7}{2}$ 上，顶点D₁、D₂、D₃、…、D_n在x轴上，则第n个阴影小正方形的面积为．

查看试题解析

三、解答题：

19. 计算： $\sqrt{4}$ +（ $\frac{1}{2}$ ）^﹣¹﹣2cos60°+（2﹣π）⁰ ．

查看试题解析
20. 解不等式组 ${\begin{matrix} 2 - x \leq 2 (x + 4) \\ x < \frac{x - 1}{3} + 1 \end{matrix}$ ，并写出该不等式组的最大整数解．

查看试题解析
21. 先化简，再求值：（ $\frac{b}{a + b}$ + $\frac{b}{a - b}$ ）÷ $\frac{a}{a^{2} - b^{2}}$ ，其中a=2017，b= $\sqrt{2}$ ．

查看试题解析
22. 有三个质地、大小都相同的小球分别标上数字2，﹣2，3后放入一个不透明的口袋搅匀，任意摸出一个小球，记下数字a后，放回口袋中搅匀，再任意摸出一个小球，又记下数字b．这样就得到一个点的坐标（a，b）．

(1)、求这个点（a，b）恰好在函数y=﹣x的图象上的概率．（请用“画树状图”或“列表”等方法给出分析过程，并求出结果）

(2)、如果再往口袋中增加n（n≥1）个标上数字2的小球，按照同样的操作过程，所得到的点（a，b）恰好在函数y=﹣x的图象上的概率是（请用含n的代数式直接写出结果）．

查看试题解析
23.
如图，在平面直角坐标系中，矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB，

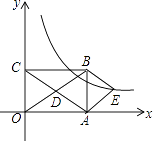(1)、求证：四边形AEBD是菱形；

(2)、如果OA=3，OC=2，求出经过点E的反比例函数解析式．

查看试题解析
24. 宁波轨道交通4号线已开工建设，计划2020年通车试运营．为了了解镇民对4号线地铁票的定价意向，某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查，并将调查结果整理后制成了如下统计图，根据图中所给出的信息解答下列问题：

(1)、求本次调查中该兴趣小组随机调查的人数；

(2)、请你把条形统计图补充完整；

(3)、如果在该镇随机咨询一位居民，那么该居民支持“起步价为2元或3元”的概率是

(4)、假设该镇有3万人，请估计该镇支持“起步价为3元”的居民大约有多少人？

查看试题解析
25. 随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位不断增加．

(1)、该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个，求该市这两年（从2013年度到2015年底）拥有的养老床位数的平均年增长率；

(2)、若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间（1个养老床位），双人间（2个养老床位），三人间（3个养老床位），因实际需要，单人间房间数在10至30之间（包括10和30），且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为t．
①若该养老中心建成后可提供养老床位200个，求t的值；
②求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？

查看试题解析
26. 如图，在△ABC中，∠C=90°，D、F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，过F作FG⊥BC于点G，其中∠OFE= $\frac{1}{2}$ ∠A．

(1)、求证：BC是⊙O的切线；

(2)、若sinB= $\frac{3}{5}$ ，⊙O的半径为r，求△EHG的面积（用含r的代数式表示）．

查看试题解析
27. 在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．

(1)、
如图1，若点F与点A重合，求证：AC=BC；

(2)、
若∠DAF=∠DBA，
①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；

②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．

查看试题解析
28.
已知：如图一，抛物线y=ax²+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x﹣2经过A、C两点，且AB=2．

(1)、求抛物线的解析式；

(2)、
若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s= $\frac{E D + O P}{E D \cdot O P}$ ，当t为何值时，s有最小值，并求出最小值．

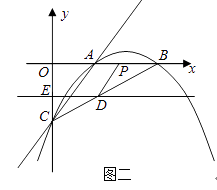(3)、在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．

查看试题解析

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1

x	…	﹣5	﹣4	﹣3	﹣2	﹣1	…
y	…	3	﹣2	﹣5	﹣6	﹣5	…