2017年江苏省连云港市灌南县中考数学一模试卷

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

1. 下面的数中，与﹣2的和为0的是（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算正确的是（　　）

A、a²+a²=a⁴ B、（a²）³=a⁵ C、2a﹣a=2 D、（ab）²=a²b²

查看试题解析
3. 四名运动员参加了射击预选赛，他们成绩的平均环数 $\bar{x}$ 及其方差s²如表所示．如果选出一个成绩较好且状态稳定的人去参赛，那么应选（）

甲
乙
丙
丁
$\bar{x}$
7
8
8
7
S²
1
1
1.2
1.8

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 无理数a满足：2＜a＜3，那么a可能是（　　）

A、 $\sqrt{10}$ B、 $\sqrt{6}$ C、2.5 D、 $\frac{20}{7}$

查看试题解析
5. 若等腰三角形的两边长为3和7，则该等腰三角形的周长为（　　）

A、10 B、13 C、17 D、13或17

查看试题解析
6. 如图，A、B、C三点在⊙O上，若∠B=53°，∠A=21°，则∠AOB等于（）

A、32° B、53° C、64° D、74°

查看试题解析
7. 如图，在平面直角坐标系中，点B、C在y轴上，△ABC是等边三角形，AB=4，AC与x轴的交点D为AC边的中点，则点D的坐标为（）

A、（1，0） B、（2 $\sqrt{3}$ ，0） C、（2，0） D、（ $\sqrt{3}$ ，0）

查看试题解析
8. 如图，抛物线y₁=a（x+2）²﹣3与y₂= $\frac{1}{2}$ （x﹣3）²+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：
①无论x取何值，y₂的值总是正数；
②a=1；
③当x=0时，y₂﹣y₁=4；
④2AB=3AC；
其中正确结论是（）

A、①② B、②③ C、③④ D、①④

查看试题解析

二、填空题

9. | $\sqrt{5} - 3$ ︳的相反数是（用代数式表示）．

查看试题解析
10. 式子 $\frac{1}{x + 1}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
11. 已知某种纸一张的厚度为0.0089cm，用科学记数法表示这个数为．

查看试题解析
12. 已知m²+m﹣1=0，则m³+2m²+2017= ．

查看试题解析
13. 计算 $\frac{3}{\sqrt{2}}$ ﹣ $\sqrt{\frac{1}{2}}$ + $\sqrt{2}$ 的结果是．

查看试题解析
14. 若一个圆锥的侧面展开图是一个半径为10cm，圆心角为144°的扇形，则该圆锥的底面半径为 cm．

查看试题解析
15. 如图，点E（0，3），O（0，0），C（4，0）在⊙A上，BE是⊙A上的一条弦．则sin∠OBE= ．

查看试题解析
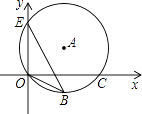16. 如图，在菱形ABCD中，∠BAD=120°，BC=1，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为．

查看试题解析

三、解答题

17. 计算（ $\sqrt{3}$ ﹣1）⁰﹣3tan30°+（ $\frac{1}{2}$ ）^﹣²+|1﹣ $\sqrt{3}$ |

查看试题解析
18. 求不等式组 ${\begin{matrix} 2 x + 1 > 0 \\ x > 2 x - 5 \end{matrix}$ 的正整数解．

查看试题解析
19. 先化简，再求值：（x﹣1）÷（ $\frac{2}{x + 1}$ ﹣1），其中x为方程x²+3x+2=0的根．

查看试题解析
20.
某厂为了解工人在单位时间内加工同一种零件的技能水平，随机抽取了50名工人加工的零件进行检测，统计出他们各自加工的合格品数是1到8这八个整数，现提供统计图的部分信息如图．
请解答下列问题：

(1)、根据统计图，写出这50名工人加工出的合格品数的中位数．

(2)、写出这50名工人加工出合格品数的众数的可能取值．

(3)、厂方认定，工人在单位时间内加工出的合格品数不低于2件为技能合格，否则，将接受技能再培训，已知该厂有同类工人400名，请估计该厂将接受技能再培训的人数．

查看试题解析
21. 已知电流在一定时间段内正常通过电子元件的概率是0.5，用列表或画树状图的方法分别求在一定时间段内，A、B之间和C、D之间电流能够正常通过的概率．（提示：可用1、0分别表示电子元件的通与不通两种状态）

查看试题解析
22. 如图，平行四边形ABCD中，AC与BD相交于点O，AB=AC，延长BC到点E，使CE=BC，连接AE，分别交BD、CD于点F、G．

(1)、求证：△ADB≌△CEA；

(2)、若BD=9，求AF的长．

查看试题解析
23. 某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为多少米？（结果精确到0.1．参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）

查看试题解析
24. 已知梯形ABCD，请使用无刻度直尺画图．

(1)、
在图1中画出一个与梯形ABCD面积相等，且以CD为边的三角形；

(2)、
图2中画一个与梯形ABCD面积相等，且以AB为边的平行四边形．

查看试题解析
25. 如图，反比例函数y= $\frac{k}{x}$ 与一次函数y=ax+b的图象交于点A（2，2）、B（ $\frac{1}{2}$ ，n）．

(1)、求这两个函数解析式；

(2)、将一次函数y=ax+b的图象沿y轴向下平移m个单位，使平移后的图象与反比例函数y= $\frac{k}{x}$ 的图象有且只有一个交点，求m的值．

查看试题解析
26. 如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．

(1)、求证：AB=BE；

(2)、若PA=2，cosB= $\frac{3}{5}$ ，求⊙O半径的长．

查看试题解析
27.
若两条抛物线的顶点相同，则称它们为“友好抛物线”，已知抛物线C₁：y₁=﹣x²+ax+b与抛物线C₂：y₂=2x²+4x+6为“友好抛物线”，抛物线C₁与x轴交于点A、C，与y轴交于点B．

(1)、求抛物线C₁的表达式．

(2)、
若F（t，0）（﹣3＜t＜0）是x轴上的一点，过点F作x轴的垂线交抛物线与点P，交直线AB于点E，过点P作PD⊥AB于点D．
①是否存在点F，使PE+PD的值最大，若存在，请求出t的值；若不存在，请说明理由．
②连接PA，以AP为边作图示一侧的正方形APMN，随着点F的运动，正方形的大小、位置也随之改变．当正方形APMN中的边MN与y轴有且仅有一个交点时，求t的取值范围．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	8	8	7
S²	1	1	1.2	1.8