2017年江苏省连云港市灌南县中考数学三模试卷

试卷更新日期：2017-07-25 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（　　）

A、a³+a³=a⁶ B、a⁶÷a³=a² C、（a²）³=a⁸ D、a²•a³=a⁵

查看试题解析
3. 在实数 $\frac{22}{7}$ ， 0，﹣ $\sqrt{2}$ ， 2π中，无理数的个数有（　　）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 如图是由3个相同的正方体组成的一个立体图形，它的三视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，数轴上的A、B、C三点所表示的数分别为a、b、c，AB=BC，则下列关系正确的是（）

A、a+c=2b B、b＞c C、c﹣a=2（a﹣b） D、a=c

查看试题解析
6. 某种衬衫的价格经过连续两次的降价后，由每件150元降到96元，则平均每次降价的百分率是（　　）

A、10% B、15% C、20% D、30%

查看试题解析
7. 如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交 $\hat{B C}$ 于点D，连接CD、OD，以下三个结论：①AC∥OD；②AC=2CD；③线段CD是CE与CO的比例中项，其中所有正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
8. 如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数 $y = \frac{k}{x}$ 的图象经过点D，四边形BCFG的面积为8，则k的值为（）

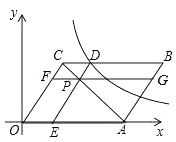A、16 B、20 C、24 D、28

查看试题解析

二、填空题

9. 分解因式：ax²﹣2ax+a=

查看试题解析
10. 抛物线y=（x+1）²﹣2的顶点坐标是．

查看试题解析
11. 若（7x﹣a）²=49x²﹣bx+9，则|a+b|= ．

查看试题解析
12. 如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直角边分别交直线b于B、C两点．若∠1=50°，则∠2的度数是°．

查看试题解析
13. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则sin∠ABC的值等于．

查看试题解析
14.
如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x﹣6上时，线段BC扫过的面积为 cm² ．

查看试题解析
15. 如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．若点D与圆心O不重合，∠BAC=25°，则∠DCA的度数为度．

查看试题解析
16. 如图，已知直线y= $\frac{3}{4}$ x﹣3与x轴、y轴分别交于A、B两点，P在以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB，则△PAB面积的最大值是．

查看试题解析

三、解答题

17. 计算：（ $\frac{1}{2}$ ）^﹣¹﹣（π﹣2）⁰+| $\sqrt{3}$ ﹣2|+sin60°．

查看试题解析
18. 解不等式组 ${\begin{matrix} 4 (x - 1) \leq 3 (x + 2) \\ \frac{x - 1}{2} < x - 4 \end{matrix}$ ．

查看试题解析
19. 先化简，再求值： $(1 - \frac{1}{a - 1}) \div \frac{a^{2} - 4 a + 4}{a^{2} - a}$ ，其中﹣2＜a≤2，请选择一个a的合适整数代入求值．

查看试题解析
20. 某校举行春季运动会，需要在初三年级选取1或2名同学作为志愿者，初三（5）班的小熊、小乐和初三（6）班的小矛、小管4名同学报名参加．

(1)、若从这4名同学中随机选取1名志愿者，则被选中的这名同学恰好是初三（5）班同学的概率是；

(2)、若从这4名同学中随机选取2名志愿者，请用列举法（画树状图或列表）求这2名同学恰好都是初三（6）班同学的概率．

查看试题解析
21.
在平面直角坐标系xOy，直线y=x﹣1与y轴交于点A，与双曲线y= $\frac{k}{x}$ 交于点B（m，2）．

(1)、求点B的坐标及k的值；

(2)、将直线AB平移，使它与x轴交于点C，与y轴交于点D，若△ABC的面积为6，求直线CD的表达式．

查看试题解析
22.
某校为了了解九年级学生（共450人）的身体素质情况，体育老师对九（1）班的50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制了如下部分频数分布表和部分频数分布直方图．
组别
次数x
频数（人数）
A
80≤x＜100
6
B
100≤x＜120
8
C
120≤x＜140
m
D
140≤x＜160
18
E
160≤x＜180
6
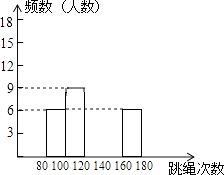
请结合图表解答下列问题：

(1)、表中的m=；

(2)、请把频数分布直方图补完整；

(3)、这个样本数据的中位数落在第组；

(4)、若九年级学生一分钟跳绳次数（x）合格要求是x≥120，则估计九年级学生中一分钟跳绳成绩不合格的人数．

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•

(1)、求证：△ABD≌△ECB；

(2)、若∠EDC=65°，求∠ECB的度数；

(3)、若AD=3，AB=4，求DC的长．

查看试题解析
24. 如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线，交AB于点E，交CA的延长线于点F．

(1)、求证：EF⊥AB；

(2)、若∠C=30°，EF= $\sqrt{6}$ ，求EB的长．

查看试题解析
25.
如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1： $\sqrt{3}$ ，AB=10米，AE=15米．（i=1： $\sqrt{3}$ 是指坡面的铅直高度BH与水平宽度AH的比）

(1)、求点B距水平面AE的高度BH；

(2)、求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0.1米．参考数据： $\sqrt{2} \approx$ 1.414， $\sqrt{3} \approx$ 1.732）

查看试题解析
26.
如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线l∥BC，交直线CD于点F．将直线l向右平移，设平移距离BE为t（t≥0），直角梯形ABCD被直线l扫过的面积（图中阴影部分）为S，S关于t的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．
信息读取

(1)、梯形上底的长AB=；

(2)、直角梯形ABCD的面积=；
图象理解

(3)、写出图②中射线NQ表示的实际意义；

(4)、当2＜t＜4时，求S关于t的函数关系式；
问题解决

(5)、当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1：3．

查看试题解析
27.
已知：如图，抛物线y=ax²﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）．

(1)、求该抛物线的解析式；

(2)、点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；

(3)、若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

组别	次数x	频数（人数）
A	80≤x＜100	6
B	100≤x＜120	8
C	120≤x＜140	m
D	140≤x＜160	18
E	160≤x＜180	6