山西省大同市2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-10 类型:期中考试
一、单选题
-
1. 下列方程中,关于x的一元二次方程是( )A、x2+2y=1 B、 ﹣2=0 C、ax2+bx+c=0 D、x2+2x=12. 在艺术字中,有些字母是中心对称图形,下面的5个字母中,是中心对称图形的有( )
 A、2个 B、3个 C、4个 D、5个3. , , 是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 抛物线 的顶点坐标为( )A、(-2, 2) B、(2, -2) C、(2, 2) D、(-2, -2)5. 将抛物线 向左平移2个单位,再向下平移3个单位,所得抛物线是( )A、 B、 C、 ﹣3 D、6. 刚刚过去的2018年国庆黄金周,越来越多的外地游客选择来大同游古城、赏美景、品美食、观民俗.小明从大同市旅游局获悉,国庆长假期间,我市共接待海内外游客约900万人次,若每年增长率不变,预计2020年国庆黄金周我市可接待海内外游客约1600万人次.问:年增长率约为( )A、 B、 C、 D、7. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
A、2个 B、3个 C、4个 D、5个3. , , 是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 抛物线 的顶点坐标为( )A、(-2, 2) B、(2, -2) C、(2, 2) D、(-2, -2)5. 将抛物线 向左平移2个单位,再向下平移3个单位,所得抛物线是( )A、 B、 C、 ﹣3 D、6. 刚刚过去的2018年国庆黄金周,越来越多的外地游客选择来大同游古城、赏美景、品美食、观民俗.小明从大同市旅游局获悉,国庆长假期间,我市共接待海内外游客约900万人次,若每年增长率不变,预计2020年国庆黄金周我市可接待海内外游客约1600万人次.问:年增长率约为( )A、 B、 C、 D、7. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.268. 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )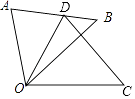 A、40° B、30° C、38° D、15°9. 如图,四边 内接于 ,若 ,则 的度数为( )
A、40° B、30° C、38° D、15°9. 如图,四边 内接于 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( )
A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正确的个数有( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知关于 的方程 的一个根为0,则 .12. 在平面直角坐标系内,若点 和点 关于原点对称,则 的值为 .13. 在二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:
x
…
﹣2
﹣1
1
2
3
…
y
…
8
3
﹣1
0
3
…
则利用二次函数的图象性质,可知该二次函数y=ax2+bx+c(a≠0)图象的对称轴是 .
14. 如图①是一座石拱桥,它是一个横断面为抛物线形状的拱桥,若桥拱的最大高度为16米,跨度为40米,图②为它在坐标系中的示意图,则抛物线的解析式是(写出顶点式和一般式均可). 15. 如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB= .
15. 如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB= .
三、解答题
-
16. 计算:(1)、解方程(2)、解方程17. △ABC在平面直角坐标系xOy中的位置如图所示.
 (1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)18. 已知关于x的方程x2+mx+m-2=0.(1)、若此方程的一个根为1,求m的值;(2)、求证:不论m取何实数,此方程都有两个不相等的实数根.19. 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为 的住房墙,另外三边用 长的建筑材料围成,所围矩形猪舍的长、宽分别为多少时,猪舍面积为 ?
(1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)18. 已知关于x的方程x2+mx+m-2=0.(1)、若此方程的一个根为1,求m的值;(2)、求证:不论m取何实数,此方程都有两个不相等的实数根.19. 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为 的住房墙,另外三边用 长的建筑材料围成,所围矩形猪舍的长、宽分别为多少时,猪舍面积为 ? 20. 已知 是 的直径,弦 与 相交, 为 的中点.(1)、求 的大小;(2)、若 , ,求 的长.21. 2018年是我市脱贫攻坚决战决胜的关键之年,阳高灵丘、云州三县区要在今年实现脱贫摘帽.近年来,享有“中国黄花之乡的云州区坚持把产业扶贫作为扶贫攻坚的重要支撑,黄花销售也成为区政府关注的一项民生工程.现有成本为每千克80元的大同特级黄花菜干货,经市场分析,若按每千克100元销售,一个月能售出800千克;销售单价每涨价1元,月销售量就减少10千克.针对黄花菜的销售情况,请解答以下问题.(1)、现计划在月销售成本不超过40000元的情况下,使得月销售利润达到24000元,销售单价应定为多少元?(2)、定价为多少元时,农民销售可获得最大利润?22. 在 中, , 是 边上的高.
20. 已知 是 的直径,弦 与 相交, 为 的中点.(1)、求 的大小;(2)、若 , ,求 的长.21. 2018年是我市脱贫攻坚决战决胜的关键之年,阳高灵丘、云州三县区要在今年实现脱贫摘帽.近年来,享有“中国黄花之乡的云州区坚持把产业扶贫作为扶贫攻坚的重要支撑,黄花销售也成为区政府关注的一项民生工程.现有成本为每千克80元的大同特级黄花菜干货,经市场分析,若按每千克100元销售,一个月能售出800千克;销售单价每涨价1元,月销售量就减少10千克.针对黄花菜的销售情况,请解答以下问题.(1)、现计划在月销售成本不超过40000元的情况下,使得月销售利润达到24000元,销售单价应定为多少元?(2)、定价为多少元时,农民销售可获得最大利润?22. 在 中, , 是 边上的高.问题发现:
(1)、如图1,
若 ,点 是线段 上一个动点(点 不与点 , 重合)连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接 ,我们会发现 、 、 之间的数量关系是 ,请你证明这个结论;
提出猜想:
(2)、如图2
若 ,点 是线段 上一个动点(点 不与点 , 重合)连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接 ,猜想线段 、 、 之间的数量关系是;
拓广探索:
(3)、若 , ( 为常数),点 是线段 上一个动点(点 不与点 , 重合),连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,连接 .请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答. 23. 如图1,抛物线 与 轴交于 、 两点,与 轴交于点 ,顶点为点 .
23. 如图1,抛物线 与 轴交于 、 两点,与 轴交于点 ,顶点为点 . (1)、求这条抛物线的解析式及直线 的解析式;(2)、 段 上一动点(点 不与点 、 重合),过点 向 轴引垂线,垂足为 ,设 的长为 ,四边形 的面积为 .求 与 之间的函数关系式及自变量 的取值范围;(3)、在线段 上是否存在点 ,使 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求这条抛物线的解析式及直线 的解析式;(2)、 段 上一动点(点 不与点 、 重合),过点 向 轴引垂线,垂足为 ,设 的长为 ,四边形 的面积为 .求 与 之间的函数关系式及自变量 的取值范围;(3)、在线段 上是否存在点 ,使 为等腰三角形?若存在,请直接写出点 的坐标;若不存在,请说明理由.