山西省吕梁市交城县2019-2020学年九年级上学期数学期中考试试卷

试卷更新日期：2019-12-10 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线 $y = - 2 {(x + 3)}^{2} - 4$ 的顶点坐标是 $($ 　　 $)$

A、 $(- 4 ， 3)$ B、 $(- 4 ， - 3)$ C、 $(3 ， - 4)$ D、 $(- 3 ， - 4)$

查看试题解析
2. 下列手机软件图标中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 方程 $x (x - 6) = 0$ 的解是（）

A、 $x = 6$ B、 $x_{1} = 0 ， x_{2} = 6$ C、 $x = - 6$ D、 $x_{1} = 0 ， x_{2} = - 6$

查看试题解析
4. △ABO与△ $A_{1} B_{1} O$ 在平面直角坐标系中关于原点O成中心对称，点A与点 $A_{1}$ 是对应点，其中点A(4，2)，则点 $A_{1}$ 的坐标是（）

A、(4，-2) B、(-4，-2) C、(-2，-3) D、(-2，-4)

查看试题解析
5. 将抛物线 $y = x^{2} - 2$ 向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为：（）

A、 $y = {(x + 2)}^{2} - 2$ B、 $y = {(x + 2)}^{2} - 5$ C、 $y = {(x - 2)}^{2} + 5$ D、 $y = {(x - 2)}^{2} - 2$

查看试题解析
6. 如图是二次函数y＝﹣x²+2x+4的图象，使y≥1成立的x的取值范围是(　　)

A、﹣1≤x≤3 B、x≤﹣1 C、x≥1 D、x≤﹣1或x≥3

查看试题解析
7. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=42°，则∠ABC的度数是（）

A、21° B、24° C、42° D、48°

查看试题解析
8. 某商品的进价为每件40元，当售价为每件80元时，每星期可卖出200件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出8件，店里每周利润要达到8450元．若设店主把该商品每件售价降低x元，则可列方程为（　　）

A、 $(80 - x) (200 + 8 x) = 8450$ B、 $(40 - x) (200 + 8 x) = 8450$ C、 $(40 - x) (200 + 40 x) = 8450$ D、 $(40 - x) (200 + x) = 8450$

查看试题解析
9. 如图，在等边三角形ABC 中，D是边AC上一点，连接BD，将ΔBCD绕点B逆时针旋转60°，得到ΔBAE，连接ED．若BC=5，BD=4.5，则下列结论错误的是（）

A、AE∥BC B、∠ADE=∠BDC C、ΔBDE是等边三角形 D、ΔADE的周长是9.5

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ ( $a \neq 0$ )的图象如图所示，分析下列四个结论：① $a b c < 0$ ；② $b^{2} - 4 a c > 0$ ；③ $2 a - b > 0$ ；④ ${(a + c)}^{2} < b^{2}$ .其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

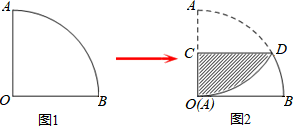
11. 若将二次函数y=x²-2x+3配方为y=（x-h）²+k的形式，则y= ．

查看试题解析
12. 若关于 $x$ 的一元二次方程 $k^{2} x^{2} + (2 k - 1) x + 1 = 0$ 有实数根，则 $k$ 的取值范围是.

查看试题解析
13. 如图1，一个扇形纸片的圆心角为90°，半径为6．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为． (答案用根号表示)

查看试题解析
14. 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形 $O A_{1} B_{1} C_{1}$ ，依此方式，绕点O连续旋转2018次得到正方形 $O A_{2018} B_{2018} C_{2018}^{}$ ，如果点A的坐标为(1，0)，那么点 $B {}_{2018}$ 的坐标是.

查看试题解析

15. 已知二次函数

y = a x^{2} + b x - 3

自变量

x

的部分取值和对应函数值

y

如下表

x	…	-2	-1	0	1	2	3	…
y	…	5	0	-3	-4	-3	0	…

若关于 $x$ 的一元二次方程 $a x^{2} + b x - m = 0$ 在实数范围内有解，则实数 $m$ 的最小值为.

查看试题解析

三、解答题

16. 解下列方程

(1)、 $x (x - 2) + x - 2 = 0$

(2)、 $2 x^{2} - x - 1 = 0$

查看试题解析
17. 如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．

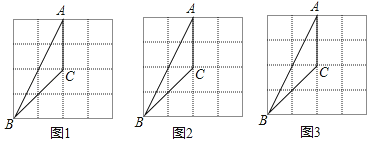(1)、在图1中，画出一个与△ABC成中心对称的格点三角形；

(2)、在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；

(3)、在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．

查看试题解析
18. 已知二次函数 $y = 2 (x - 1) (x - m - 3)$ （ $m$ 为常数）.

(1)、求证：不论 $m$ 为何值，该函数的图象与 $x$ 轴总有公共点；

(2)、当 $m$ 取什么值时，该函数的图象与 $y$ 轴的交点在 $x$ 轴的上方？

查看试题解析
19. 为了节省材料，某水产养殖户利用水库的岸堤(岸堤足够长)为一边，用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域，而且AE：BE=2：1.设BC的长度是 $x$ 米，矩形区域ABCD的面积为 $y$ 平方米.

(1)、求 $y$ 与 $x$ 之间的函数关系式，并注明自变量 $x$ 的取值范围；

(2)、 $x$ 取何值时， $y$ 有最大值？最大值是多少？

查看试题解析
20. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．

(1)、若∠ADE=25°，求∠C的度数；

(2)、若AB=AC，CE=2，求⊙O半径的长．

查看试题解析
21. 某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

(1)、求水柱所在抛物线（第一象限部分）的函数表达式；

(2)、王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

(3)、经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

查看试题解析
22. 实践与探究
在平面直角坐标系中，四边形AOBC是矩形，点 $O$ (0，0)，点A(5，0)，点B(0，3).以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F.

(1)、如图(1)，当点D落在BC边上时，求点D的坐标；

(2)、如图(2)，当点D落在线段BE上时，AD与BC交于点H.

①求证：ΔADB≌ΔAOB；

②求点H的坐标.

查看试题解析
23. 综合与探究
如图，抛物线 $y = x^{2} + b x + c$ 的图象经过坐标原点O，且与 $x$ 轴的另一交点为( $- \frac{\sqrt{3}}{3}$ ，0).

(1)、求抛物线的解析式；

(2)、若直线 $y = \frac{\sqrt{3}}{3} x + \frac{4}{3}$ 与抛物线相交于点A和点B(点A在第二象限)，设点A′是点A关于原点O的对称点，连接A′B，试判断ΔAA′B的形状，并说明理由；

(3)、在问题(2)的基础上，探究：平面内是否存在点P，使得以点A，B，A′，P为顶点的四边形是菱形？若存在直接写出点P的坐标；若不存在，请说明理由.

查看试题解析