山西省晋中市灵石县2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-10 类型:期中考试
一、单选题
-
1. 解一元二次方程x2+4x-1=0,配方正确的是( )A、 B、 C、 D、2. 通过大量重复抛掷两枚均匀硬币的试验,出现两个反面的成功率大约稳定在A、 B、 C、 D、3. 如图,DE是△ABC的中位线,已知△ABC的面积为8 ,则△ADE的面积为( ) .
 A、2 B、4 C、6 D、84. 沿圆柱体上底面直径截去一部分后的物体如图所示,它的俯视图是( )
A、2 B、4 C、6 D、84. 沿圆柱体上底面直径截去一部分后的物体如图所示,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图已知关于x的函数y=k(x-1)和y=- (k≠0),它们在同一坐标系内的图象大致是( )A、
5. 如图已知关于x的函数y=k(x-1)和y=- (k≠0),它们在同一坐标系内的图象大致是( )A、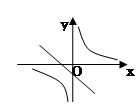 B、
B、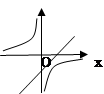 C、
C、 D、
D、 6. 方程x2﹣2x﹣4=0的根的情况( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根7. 在反比例函数y= 图象上有三个点A(x1 , y1)、B(x2 , y2)、C(x3 , y3),若x1<0<x2<x3 , 则下列结论正确的是( )A、y1<y3<y2 B、y2<y3<y1 C、y3<y1<y2 D、y3<y2<y18. 如图,A 、 B是曲线 上的点,经过A、 B两点向x 轴、y轴作垂线段,若S阴影=1 则 S1+S2 =( )
6. 方程x2﹣2x﹣4=0的根的情况( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根7. 在反比例函数y= 图象上有三个点A(x1 , y1)、B(x2 , y2)、C(x3 , y3),若x1<0<x2<x3 , 则下列结论正确的是( )A、y1<y3<y2 B、y2<y3<y1 C、y3<y1<y2 D、y3<y2<y18. 如图,A 、 B是曲线 上的点,经过A、 B两点向x 轴、y轴作垂线段,若S阴影=1 则 S1+S2 =( ) A、4 B、5 C、6 D、89. 点 是线段 的黄金分割点,且 ,则 的长为( )A、 B、 C、 或 D、 或10. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )
A、4 B、5 C、6 D、89. 点 是线段 的黄金分割点,且 ,则 的长为( )A、 B、 C、 或 D、 或10. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )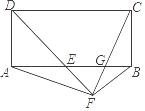 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,根据图象写出反比例函数的解析式.
 12. 在一次新年聚会中,小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.13. 若a︰b︰c=2︰3︰4,且2a+3b-c=18,则a+2b+c=14. 如图,在平面直角坐标系中,△OAB与△OCD是以原点O为位似中心的位似图形,且位似比为1:3,已知点A的坐标为(1,2),则点C的坐标是 .
12. 在一次新年聚会中,小朋友们互相赠送礼物,全部小朋友共互赠了110件礼物,若假设参加聚会小朋友的人数为x人,则根据题意可列方程为.13. 若a︰b︰c=2︰3︰4,且2a+3b-c=18,则a+2b+c=14. 如图,在平面直角坐标系中,△OAB与△OCD是以原点O为位似中心的位似图形,且位似比为1:3,已知点A的坐标为(1,2),则点C的坐标是 . 15. 如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为 , , ,…, 的n 个正方形依次放入△ABC中,则第n个正方形的边长 (用含n的式子表示).
15. 如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为 , , ,…, 的n 个正方形依次放入△ABC中,则第n个正方形的边长 (用含n的式子表示).
三、解答题
-
16. 解方程.(1)、(3x+2)2=25(2)、3x2﹣1=4x(3)、(2x+1)2=3(2x+1)(4)、4x2+8x+3=017. 如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
 (1)、利用画树状图或列表的方法,求甲获胜的概率.(2)、这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).18. 定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
(1)、利用画树状图或列表的方法,求甲获胜的概率.(2)、这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).18. 定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3﹣4i)=(2+3)+(i﹣4i)=5﹣3i
(1)、填空:i3= , i4= .(2)、填空:①(2+i)(2﹣i)=; ②(2+i)2= .(3)、若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知,(x+y)+3i=1﹣(x﹣y)i,(x,y为实数),求x,y的值.(4)、试一试:请利用以前学习的有关知识将 化简成a+bi的形式.(5)、解方程:x2﹣2x+4=0.19. 如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE交CD于点F . (1)、求证:△ABE∽△DEF;(2)、求EF的长.20. 如图,一次函数 的图象与反比例函数 的图象交于A(-2,-1)、B(1,n)两点。
(1)、求证:△ABE∽△DEF;(2)、求EF的长.20. 如图,一次函数 的图象与反比例函数 的图象交于A(-2,-1)、B(1,n)两点。 (1)、利用图中条件求反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值大于反比例函数的值的 的取值范围.21. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
(1)、利用图中条件求反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值大于反比例函数的值的 的取值范围.21. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度. (2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
(2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度? 22. 为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
22. 为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题: (1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?23. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A , C的坐标分别为A(﹣3,0),C(1,0),BC= AC .
(1)、药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?(2)、研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?(3)、研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?23. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A , C的坐标分别为A(﹣3,0),C(1,0),BC= AC . (1)、在x轴上找一点D , 连接DB , 使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(2)、在(1)的条件下,如P , Q分别是AB和AD上的动点,连接PQ , 设AP=DQ=m , 问是否存在这样的m , 使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.
(1)、在x轴上找一点D , 连接DB , 使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(2)、在(1)的条件下,如P , Q分别是AB和AD上的动点,连接PQ , 设AP=DQ=m , 问是否存在这样的m , 使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.