福建省泉州市晋江区安海片区2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-10 类型:期中考试
一、单选题
-
1. 如图,将图形用放大镜放大,应该属于( ).
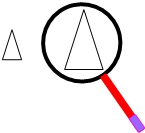 A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、3. 估计(2 +6 )× 的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间4. 满足下列条件时, 不是直角三角形的为( ).A、 B、 C、 D、5. 若关于x的方程kx2﹣x﹣ =0有实数根,则实数k的取值范围是( )A、k=0 B、k≥﹣ 且k≠0 C、k≥﹣ D、k>﹣6. 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡的坡度为( )
A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、3. 估计(2 +6 )× 的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间4. 满足下列条件时, 不是直角三角形的为( ).A、 B、 C、 D、5. 若关于x的方程kx2﹣x﹣ =0有实数根,则实数k的取值范围是( )A、k=0 B、k≥﹣ 且k≠0 C、k≥﹣ D、k>﹣6. 如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡的坡度为( )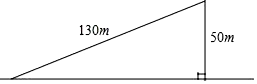 A、 B、 C、 D、7. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )
A、 B、 C、 D、7. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )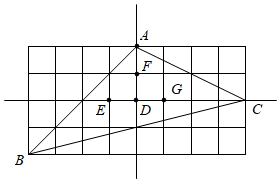 A、点 B、点 C、点 D、点8. 如图,在反比例函数 的图象上有一动点A , 连接并AO延长交图象的另一支于点B , 在第二象限内有一点C , 满足AC=BC , 当点A运动时,点C始终在函数 的图象上运动,若 ,则k的值为
A、点 B、点 C、点 D、点8. 如图,在反比例函数 的图象上有一动点A , 连接并AO延长交图象的另一支于点B , 在第二象限内有一点C , 满足AC=BC , 当点A运动时,点C始终在函数 的图象上运动,若 ,则k的值为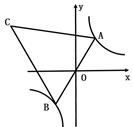 A、-3 B、-6 C、-9 D、-129. 如图,菱形 和菱形 的边长分别为4和6, ,则阴影部分的面积是( )
A、-3 B、-6 C、-9 D、-129. 如图,菱形 和菱形 的边长分别为4和6, ,则阴影部分的面积是( )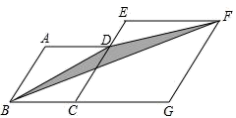 A、 B、 C、 D、10. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )
A、 B、 C、 D、10. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )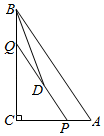 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
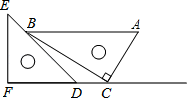
11. 分式 有意义时,x的取值范围是 .12. 化简 = .13. 已知x1 , x2是方程x2﹣x﹣3=0的两根,则 = .14. 三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是.
 15. 如图,在矩形ABCD中,AB=4,BC= ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若 = ,则CE= .
15. 如图,在矩形ABCD中,AB=4,BC= ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若 = ,则CE= .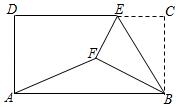 16. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.
16. 如图,由10个完全相同的正三角形构成的网格图中, 如图所示,则 =.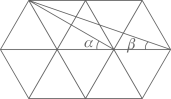
三、解答题
-
17. 计算(1)、计算:(2)、解方程: .18. 关于 的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求 的取值范围.19. 请先阅读这段内容.再解答问题
三角函数中常用公式 .求 的值,
即 .
试用公式 ,求出 的值.
20. 如图,△ABC中,∠ACB>∠ABC .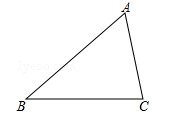 (1)、用直尺和圆规在∠ACB的内部作射线CM , 使∠ACM=∠ABC(不要求写作法,保留作图痕迹);(2)、若(1)中的射线CM交AB于点D , AB=9,AC=6,求AD的长.21. 江苏是全国首个自然村“村村通宽带”省份.我市某村为了将当地农产品外销,建立了淘宝网店.该网店于今年7月底以每袋25元的成本价收购一批农产品.当商品售价为每袋40元时,8月份销售256袋.9、10月该商品十分畅销.销售量持续走高.在售价不变的基础上,10月份的销售量达到400袋.设9、10这两个月月平均增长率不变.(1)、求9、10这两个月的月平均增长率;(2)、为迎接双“十一”,11月份起,该网店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/每袋,销售量就增加5袋,当农产品每袋降价多少元时,该淘宝网店11月份获利4250元?22. 如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据: ≈1.41, ≈1.73)
(1)、用直尺和圆规在∠ACB的内部作射线CM , 使∠ACM=∠ABC(不要求写作法,保留作图痕迹);(2)、若(1)中的射线CM交AB于点D , AB=9,AC=6,求AD的长.21. 江苏是全国首个自然村“村村通宽带”省份.我市某村为了将当地农产品外销,建立了淘宝网店.该网店于今年7月底以每袋25元的成本价收购一批农产品.当商品售价为每袋40元时,8月份销售256袋.9、10月该商品十分畅销.销售量持续走高.在售价不变的基础上,10月份的销售量达到400袋.设9、10这两个月月平均增长率不变.(1)、求9、10这两个月的月平均增长率;(2)、为迎接双“十一”,11月份起,该网店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/每袋,销售量就增加5袋,当农产品每袋降价多少元时,该淘宝网店11月份获利4250元?22. 如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据: ≈1.41, ≈1.73) 23. 在平面直角坐标系中,已知 , ,点 从点 开始沿 边向点 以 的速度移动;点 从点 开始沿 边向点 以 的速度移动.如果 、 同时出发,用 表示移动的时间 ,
23. 在平面直角坐标系中,已知 , ,点 从点 开始沿 边向点 以 的速度移动;点 从点 开始沿 边向点 以 的速度移动.如果 、 同时出发,用 表示移动的时间 , (1)、用含 的代数式表示:线段 ; ; .(2)、当 与 相似时,求出 的值.24. 如图,正方形 、等腰 的顶点 在对角线 上(点 与 、 不重合), 与 交于 , 延长线与 交于点 ,连接 .
(1)、用含 的代数式表示:线段 ; ; .(2)、当 与 相似时,求出 的值.24. 如图,正方形 、等腰 的顶点 在对角线 上(点 与 、 不重合), 与 交于 , 延长线与 交于点 ,连接 . (1)、求证: .(2)、求证:(3)、若 ,求 的值.25. 已知:如图,在四边形 中, , , , , 垂直平分 .点 从点 出发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为 ;当一个点停止运动,另一个点也停止运动.过点 作 ,交 于点 ,过点 作 ,分别交 , 于点 , .连接 , .设运动时间为 ,解答下列问题:
(1)、求证: .(2)、求证:(3)、若 ,求 的值.25. 已知:如图,在四边形 中, , , , , 垂直平分 .点 从点 出发,沿 方向匀速运动,速度为 ;同时,点 从点 出发,沿 方向匀速运动,速度为 ;当一个点停止运动,另一个点也停止运动.过点 作 ,交 于点 ,过点 作 ,分别交 , 于点 , .连接 , .设运动时间为 ,解答下列问题: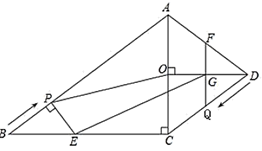 (1)、当 为何值时,点 在 的平分线上?(2)、设四边形 的面积为 ,求 与 的函数关系式.(3)、连接 , ,在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.
(1)、当 为何值时,点 在 的平分线上?(2)、设四边形 的面积为 ,求 与 的函数关系式.(3)、连接 , ,在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.