2016-2017学年江西省赣州市十四县（市）联考高二下学期期中数学试卷（文科）

试卷更新日期：2017-07-24 类型：期中考试

进入出卷网下载

一、选择题

1. 设i是虚数单位，则复数z= $\frac{1 + 3 i}{1 - 2 i}$ 的共轭复数 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 用反证法证明命题“若自然数a，b，c的积为偶数，则a，b，c中至少有一个偶数”时，对结论正确的反设为（）

A、a，b，c中至多有一个偶数 B、a，b，c都是奇数 C、a，b，c至多有一个奇数 D、a，b，c都是偶数

查看试题解析
3. 两个变量y与x的回归模型中，分别选择了4个不同模型，它们对应的回归系数r如下，其中变量之间线性相关程度最高的模型是（）

A、模型1对应的r为﹣0.98 B、模型2对应的r为0.80 C、模型3对应的r为0.50 D、模型4对应的r为﹣0.25

查看试题解析
4. 若关于x的不等式|x﹣m|+|x+2|＞4的解集为R，则实数m的取值范围是（）

A、（﹣2，6） B、（﹣∞，﹣6）∪（2，+∞） C、（﹣∞，﹣2）∪（6，+∞） D、（﹣6，2）

查看试题解析
5. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁、F₂ ，直线y= $\frac{\sqrt{5}}{3}$ b与椭圆C交于A、B两点．若四边形ABF₂F₁是矩形，则椭圆C的离心率为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 已知复数z=（3a+2i）（b﹣i）的实部为4，其中a、b为正实数，则2a+b的最小值为（）

A、2 B、4 C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
7. 如图是一个程序框图，则输出的S的值是（）

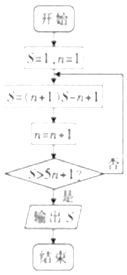A、18 B、20 C、87 D、90

查看试题解析
8. 观察下列各式： $\frac{1}{1 + 2}$ = $\frac{1}{3}$ ， $\frac{1}{1 + 2}$ + $\frac{1}{1 + 2 + 3}$ = $\frac{1}{2}$ ， $\frac{1}{1 + 2}$ + $\frac{1}{1 + 2 + 3}$ + $\frac{1}{1 + 2 + 3 + 4}$ = $\frac{3}{5}$ …，则 $\frac{1}{1 + 2}$ + $\frac{1}{1 + 2 + 3}$ +…+ $\frac{1}{1 + 2 + \dots + 12}$ 等于（）

A、 $\frac{5}{6}$ B、 $\frac{11}{12}$ C、 $\frac{11}{13}$ D、 $\frac{12}{13}$

查看试题解析
9. 已知命题p：∃x∈R，3^x^﹣³≤0．若（￢p）∧q是假命题，则命题q可以是（）

A、抛物线y= $\frac{1}{4}$ x²的焦点坐标为（0，1） B、双曲线 $\frac{x^{2}}{2}$ ﹣ $\frac{y^{2}}{6}$ =2的右顶点到其左、右焦点的距离之比为3 C、函数f（x）=x³﹣3x²+b在区间（﹣∞，﹣1）上无极值点 D、曲线f（x）=x³﹣3x²+5在点（1，f（1））处切线的倾斜角大于 $\frac{3 π}{4}$

查看试题解析
10. 已知椭圆M：（x﹣2）²+y²=4，则过点（1，1）的直线中被圆M截得的最短弦长为2 $\sqrt{2}$ ．类比上述方法：设球O是棱长为3的正方体ABCD﹣A₁B₁C₁D₁的外接球，过AC₁的一个三等分点作球O的截面，则最小截面的面积为（）

A、π B、4π C、5π D、6π

查看试题解析
11. “a≥2”是“直线l：2ax﹣y+2a²=0（a＞0）与双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{4}$ =1的右支无焦点”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
12. 若函数f（x）=lnx+ $\frac{a}{x + 1}$ （a∈N）在（1，3）上只有一个极值点，则a的取值个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 命题“若x≥1，则x²﹣4x+2≥﹣1”的否命题为．

查看试题解析
14. 复数z满足（z+2i）i=3﹣i，则|z|= ．

查看试题解析
15. 函数f（x）=﹣ $\frac{4}{5}$ x﹣cosx在[0， $\frac{π}{4}$ ]上的最大值为．

查看试题解析
16. 从焦点为F的抛物线y²=2px（p＞0）上取一点A（x₀ ， y₀）（x₀＞ $\frac{p}{2}$ ）作其准线的垂线，垂足为B，若|AF|=4，B到直线AF的距离为 $\sqrt{7}$ ，则此抛物线的方程为．

查看试题解析

三、解答题

17. 已知函数f（x）=|x﹣3|﹣5，g（x）=|x+2|﹣2．
（Ⅰ）求不等式f（x）≤2的解集；
（Ⅱ）若不等式f（x）﹣g（x）≥m﹣3有解，求实数m的取值范围．

查看试题解析
18. 设函数f（x）=|x+2|+|x﹣2|，x∈R，不等式f（x）≤6的解集为M．

(1)、求M；

(2)、当a，b∈M时，证明：3|a+b|≤|ab+9|．

查看试题解析
19. 禽流感是家禽养殖业的最大威胁．为检验某新药物预防禽流感的效果，取80只家禽进行试验，得到如下丢失数据的列联表：（c，d，M，N表示丢失的数据）
患病
未患病
总计
未服用药
a
b
40
服用药
5
d
M
总计
25
N
80

(1)、求出a，b，d，M，N的值，并判断：能否有99.5%的把握认为药物有效；

(2)、若表中服用药后患病的5只家禽分别为3只鸡和2只鸭，现从这5只家禽中随机选取2只，求这2只家禽是同一类的概率．
下面的临界值表供参考：
P（K²≥k₀）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k₀
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析
20. 已知条件p：k²+3k﹣4≤0；条件q：函数f（x）= $\frac{1}{2}$ x²+kx+lnx在定义域内递增，若p∧q为假，p∨q为真，求实数k的取值范围．

查看试题解析
21. 已知椭圆G： $\frac{x^{2}}{3 b^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（b＞0）的上、下顶点和右焦点分别为M、N和F，且△MFN的面积为4 $\sqrt{2}$ ．

(1)、求椭圆G的方程；

(2)、若斜率为1的直线l与椭圆G交于A、B两点．以AB为底作等腰三角形，顶点为P（﹣3，2），求△PAB的面积．

查看试题解析
22. 已知函数f（x）=ax﹣lnx，函数g（x）= $\frac{1}{3} b x^{3}$ ﹣bx，a∈R，b∈R且b≠0．

(1)、讨论函数f（x）的单调性；

(2)、若a=1，且对任意的x₁（1，2），总存在x₂∈（1，2），使f（x₁）+g（x₂）=0成立，求实数b的取值范围．

查看试题解析

	患病	未患病	总计
未服用药	a	b	40
服用药	5	d	M
总计	25	N	80

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828