2016-2017学年湖北省部分重点中学联考高二下学期期中数学试卷（文科）

试卷更新日期：2017-07-24 类型：期中考试

进入出卷网下载

一、选择题

1. 下列说法错误的是（）

A、若命题p∧q为假命题，则p，q都是假命题 B、已知命题p：∀x∈R，x²+x+1＞0，则￢p：∃x₀∈R，x₀²+x₀+1≤0 C、命题“若x²﹣3x+2=0，则x=1”的逆命题为：“若x≠1，则x²﹣3x+2≠0” D、“x=1”是“x²﹣3x+2=0”的充分不必要条件

查看试题解析
2. 设f（x）=xe^x的导函数为f′（x），则f′（1）的值为（）

A、e B、e+1 C、2e D、e+2

查看试题解析
3. 已知命题p：∀x∈R，ax²+2x+3＞0．若命题p为假命题，则实数a的取值范围是（）

A、{a|a＜ $\frac{1}{3}$ } B、{a|0＜a≤ $\frac{1}{3}$ } C、{a|a≤ $\frac{1}{3}$ } D、{a|a≥ $\frac{1}{3}$ }

查看试题解析
4. 已知f（x）在R上是可导函数，f（x）的图象如图所示，则不等式f′（x）＞0的解集为（）

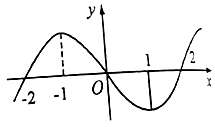A、（﹣2，0）∪（2，+∞） B、（﹣∞，2）∪（2，+∞） C、（﹣∞，﹣1）∪（1，+∞） D、（﹣2，﹣1）∪（1，2）

查看试题解析
5. 曲线f（x）=x²+2x+e^x在点（0，f（0））处的切线的方程为（）

A、y=x﹣1 B、y=x+1 C、y=3x﹣1 D、y=3x+1

查看试题解析
6. 直线y=2x+1的参数方程是（）

A、 ${\begin{matrix} x = t^{2} \\ y = 2 t^{2} + 1 \end{matrix}$ （t为参数） B、 ${\begin{matrix} x = t - 1 \\ y = 2 t - 1 \end{matrix}$ （t为参数） C、 ${\begin{matrix} x = 2 t - 1 \\ y = 4 t + 1 \end{matrix}$ （t为参数） D、 ${\begin{matrix} x = s i n θ \\ y = 2 s i n θ + 1 \end{matrix}$ （θ为参数）

查看试题解析
7. 已知f（x）=4x³﹣6x²+m（m为常数）在[﹣2，1]上有最大值5，那么此函数在[﹣2，1]上的最小值是（）

A、3 B、﹣49 C、﹣52 D、﹣51

查看试题解析
8. 函数f（x）=x（x﹣c）²在x=1处有极小值，则实数c为（）

A、3 B、1 C、1或3 D、﹣1

查看试题解析
9. 已知函数f（x）=x²+ $\frac{a}{x}$ ，则“a＜2”是“函数f（x）在（1，+∞）上为增函数”的（）

A、充分而不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
10. 若a= $\frac{l n 3}{3}$ ，b= $\frac{l n 4}{4}$ ，c= $\frac{l n 5}{5}$ ，则有（）

A、a＜b＜c B、c＜b＜a C、c＜a＜b D、b＜a＜c

查看试题解析
11. 直线x=a分别与曲线y=2（x+1），y=x+lnx交于A、B两点，则|AB|的最小值为（）

A、3 B、2 C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{3}{2}$

查看试题解析
12. 已知f（x）是定义在R上的函数，其导函数为f′（x）﹣f（x）＞1，f（0）=2016，则不等式f（x）＞2017•e^x﹣1（其中e为自然对数的底数）的解集为（）

A、（﹣∞，0）∪（0，+∞） B、（2017，+∞） C、（0，+∞） D、（0，+∞）∪（2017，+∞）

查看试题解析

二、填空题

13. 已知条件p：x≥a，q：{x|x＜﹣3或x＞3}，若p是q的充分不必要条件，则实数a的取值范围是．

查看试题解析
14. 在极坐标系中，点（2， $\frac{π}{3}$ ）到圆ρ=﹣2cosθ的圆心的距离为．

查看试题解析
15. 若函数f（x）=x³﹣3x+a有三个不同的零点，求实数a的取值范围．

查看试题解析
16. 已知函数f（x）=xlnx﹣ $\frac{a}{2}$ x²在定义域内有极值，则实数a的取值范围是．

查看试题解析

三、解答题

17. 已知命题P：方程 $\frac{x^{2}}{m^{2}}$ + $\frac{y^{2}}{2 m + 8}$ =1表示焦点在x轴上的椭圆，命题Q：曲线y=x²+（2m﹣3）x+ $\frac{1}{4}$ 与x轴交于不同的两点，如果“P∨Q”为真命题且“P∧Q”为假命题，求实数m的取值范围．

查看试题解析
18. 已知 ${(\sqrt{x} - \frac{2}{x^{2}})}^{n} (n \in N^{*})$ 的展开式中第五项的系数与第三项的系数之比是10：1

(1)、求展开式中各项系数的和

(2)、求展开式中含 $x^{\frac{3}{2}}$ 的项

(3)、求展开式中系数最大的项和二项式系数最大的项．

查看试题解析
19. 若a∈R，b∈R，且a＞0，b＞0，2c＞a+b．

(1)、综合法证明：c²＞ab；

(2)、分析法证明：c﹣ $\sqrt{c^{2} - a b}$ ＜a＜c+ $\sqrt{c^{2} - a b}$ ．

查看试题解析
20. 某商场根据调查，估计家电商品从年初（1月）开始的x个月内累计的需求量p（x）（百件）为 $p (x) = \frac{x}{2} (39 x - 2 x^{2} + 41) (1 \leq x \leq 12 且 x \in N^{*})$

(1)、求第x个月的需求量f（x）的表达式．

(2)、若第x个月的消售量满足 $g (x) = {\begin{matrix} f (x) - 21 x ， (1 \leq x < 7 ， x \in N^{*}) \\ \frac{x^{2}}{e^{x}} (\frac{1}{3} x^{2} - 10 x + 96) ， (7 \leq x \leq 12 ， x \in N^{*}) \end{matrix}$ （单位：百件），每件利润 $q (x) = \frac{100 e^{x - 6}}{x}$ 元，求该商场销售该商品，求第几个月的月利润达到最大值？最大是多少？（e⁶取值为403）

查看试题解析
21. 已知函数f（x）=x²（x﹣a），其中a∈R．

(1)、若a=1，求曲线y=f（x）的过点（1，0）的切线方程．

(2)、讨论函数y=f（x）在[0，4]上的单调性．

查看试题解析
22. 已知函数f（x）=ax﹣1﹣lnx（a∈R）．（Ⅰ）讨论函数f（x）在定义域内的极值点的个数；
（Ⅱ）若函数f（x）在x=1处取得极值，对∀x∈（0，+∞），f（x）≥bx﹣2恒成立，求实数b的取值范围；
（Ⅲ）当0＜x＜y＜e²且x≠e时，试比较 $\frac{y}{x} 与 \frac{1 - l n y}{1 - l n x}$ 的大小．

查看试题解析