2017年湖南省永州市祁阳县中考数学五模试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、选择题（本大题共10小题，每小题4分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的.）
-
1. 下列实数中，无理数是（ ）A、2 B、3.333 C、﹣π D、2. 下列计算中，结果是a6的是（ ）A、a2+a4 B、a2•a3 C、a12÷a2 D、（a2）33. 已知一粒大米的质量约为0.000021千克，这个数用科学记数法表示为（ ）A、0.21×10﹣4 B、2.1×10﹣4 C、2.1×10﹣5 D、21×10﹣64. 下列命题是假命题的是（ ）A、经过两点有且只有一条直线 B、三角形的中位线平行且等于第三边的一半 C、平行四边形的对角线相等 D、圆的切线垂直于经过切点的半径5. 在线段、角、平行四边形、矩形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是（ ）A、2个 B、3个 C、4个 D、5个6. 实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（ ）
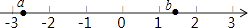A、a＞﹣2 B、a＜﹣3 C、a＞﹣b D、a＜﹣b7. 从分别标有数﹣3，﹣2，﹣1，0，1，2，3的七张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝对值不是正数的概率是（ ）A、 B、 C、 D、8. 已知反比例函数y= ，当1＜x＜2时，y的取值范围是（ ）A、y＞10 B、5＜y＜10 C、1＜y＜2 D、0＜y＜59. 如图，在边长为6的菱形ABCD中，∠DAB=60°，以点D为圆心，菱形的高DF为半径画弧，交AD于点E，交CD于点G，则图中阴影部分的面积是（ ）
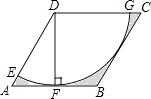A、18 ﹣9π B、18﹣3π C、9 ﹣ D、18 ﹣3π10. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是（ ）
A、43 B、45 C、51 D、53二、填空题
-
11. 若二次根式 有意义，则x的取值范围是 ．12. 在一次“爱心互助”捐款活动中，某班第一小组7名同学捐款的金额（单位：元）分别为6，7，6，15，9，6，9．这组数据的众数和中位数分别是 ．13. 钟表在12时15分时刻的时针与分针所成的角是°．14. 一个圆锥的侧面展开图是半径为6的半圆，则这个圆锥的底面半径为 ．15. 如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是 ．
16. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为 ．
17. 明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S（单位：m2）与工作时间t（单位：h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是m2 ．
18. 定义：有三个内角相等的四边形叫三等角四边形．三等角四边形ABCD中，∠A=∠B=∠C，则∠A的取值范围 ．三、解答题
-
19. 计算：|1﹣ |﹣3tan30°﹣（ ﹣5）0 ．20. 先化简，再求值：（ + ）•（x2﹣1），其中x= ．21.
如图，某学校在“国学经典”中新建了一座吴玉章雕塑，小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°，看雕塑底部C的仰角为30°，求塑像CD的高度．（最后结果精确到0.1米，参考数据： ≈1.7）
22. 今年我县中考的体育测试成绩改为等级制，即把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格．我县5月份举行了全县九年级学生体育测试．现从中随机抽取了部分学生的体育成绩，并将其绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
(1)、本次抽样测试的学生人数是；(2)、图1中∠α的度数是 ， 并把图2条形统计图补充完整；(3)、该县九年级有学生9000名，如果全部参加这次中考体育科目测试，请估算不及格的人数是多少？23. 某汽车专卖店销售A，B两种型号的新能源汽车．上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．(1)、求每辆A型车和B型车的售价各为多少元．(2)、甲公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？24. 如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CE•CA．
(1)、求证：BC=CD；(2)、分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD= ，求DF的长．25.已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．
(1)、如图1，若点P在线段AB的延长线上，求证：EA=EC；
(2)、若点P在线段AB上．①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；
②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．
26.将抛物线c1： 沿x轴翻折，得到抛物线c2 ， 如图1所示．
(1)、请直接写出抛物线c2的表达式；(2)、现将抛物线c1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x轴的交点从左到右依次为A、B；将抛物线c2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E．①当B、D是线段AE的三等分点时，求m的值；②在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由．