2017年湖北省黄冈市中考数学模拟试卷(d卷)
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 实数a,b在数轴上的位置如图所示,则下列各式正确的是( )
 A、a>b B、a>﹣b C、a<b D、﹣a<﹣b2. 下列运算正确的是( )A、(2a)2=2a2 B、a6÷a2=a3 C、(a+b)2=a2+b2 D、a3•a2=a53. 下列式子中结果为负数的是( )A、|﹣2| B、﹣(﹣2) C、﹣2﹣1 D、(﹣2)24. 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图).如果第一次转弯时的∠B=140°,那么∠C应是( )
A、a>b B、a>﹣b C、a<b D、﹣a<﹣b2. 下列运算正确的是( )A、(2a)2=2a2 B、a6÷a2=a3 C、(a+b)2=a2+b2 D、a3•a2=a53. 下列式子中结果为负数的是( )A、|﹣2| B、﹣(﹣2) C、﹣2﹣1 D、(﹣2)24. 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图).如果第一次转弯时的∠B=140°,那么∠C应是( ) A、140° B、40° C、100° D、180°5. 一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )A、m=3,n=5 B、m=n=4 C、m+n=4 D、m+n=86. 如图所示的工件的主视图是( )
A、140° B、40° C、100° D、180°5. 一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )A、m=3,n=5 B、m=n=4 C、m+n=4 D、m+n=86. 如图所示的工件的主视图是( )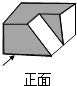 A、
A、 B、
B、 C、
C、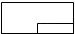 D、
D、
二、填空题
-
7. 函数y=﹣ 中自变量x的取值范围是 .8. 分解因式:2x2﹣4x+2= .9. 化简 的结果是 .10. 计算 的结果是 .11. 某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 .12. 分式方程 ﹣ =1的解是 .13. 用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为cm2 .
 14. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .
14. 如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 .
三、解答题
-
15. 解不等式组 并在数轴上表示出它的解集.16. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.
 17. 已知方程x2+2kx+k2﹣2k+1=0有两个实数根x1 , x2 .(1)、求实数k的取值范围;(2)、若x12+x22=4,求k的值.18. 某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
17. 已知方程x2+2kx+k2﹣2k+1=0有两个实数根x1 , x2 .(1)、求实数k的取值范围;(2)、若x12+x22=4,求k的值.18. 某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)、该商场购进甲、乙两种矿泉水各多少箱?(2)、全部售完500箱矿泉水,该商场共获得利润多少元?19. “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:请结合图表完成下列各题:
 (1)、①表中a的值为 , 中位数在第组;
(1)、①表中a的值为 , 中位数在第组;②频数分布直方图补充完整;
(2)、若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?(3)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
20. 如图,已知F是以AC为直径的半圆O上任一点,过AC上任一点H作AC的垂线分别交CF、AF的延长线于点E、B,DB=DE. (1)、求证:DF是⊙O的切线;(2)、若BF=AF,求证:AF2=EF•CF.21. 如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y= (k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(1)、求证:DF是⊙O的切线;(2)、若BF=AF,求证:AF2=EF•CF.21. 如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y= (k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S. (1)、求k的值;(2)、当S= 时,求P点的坐标;(3)、写出S关于m的关系式.22. 小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ≈1.41, ≈1.73供选用,结果保留整数)
(1)、求k的值;(2)、当S= 时,求P点的坐标;(3)、写出S关于m的关系式.22. 小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 ≈1.41, ≈1.73供选用,结果保留整数) 23. 校园安全与每个师生、家长和社会有着切身的关系.某校教学楼共五层,设有左、右两个楼梯口,通常在放学时,若持续不正常,会导致等待通过的人较多,发生拥堵,从而出现不安全因素.通过观察发现位于教学楼二、三楼的七年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟12人递增,6分钟后经过单个楼梯口等待人数按每分钟12人递减;位于四、五楼的八年级学生从放学时刻起,经过单个楼梯口等待人数y2与时间为t(分)满足关系式y2=﹣4t2+48t﹣96(0≤t≤12).若在单个楼梯口等待人数超过80人,就会出现安全隐患.(1)、试写出七年级学生在单个楼梯口等待的人数y1(人)和从放学时刻起的时间t(分)之间的函数关系式,并指出t的取值范围.(2)、若七、八年级学生同时放学,试计算等待人数超过80人所持续的时间.(3)、为了避免出现安全隐患,该校采取让七年级学生提前放学措施,要使单个楼梯口等待人数不超过80人,则七年级学生至少比八年级提前几分钟放学?24. 如图,在平面直角坐标系中,矩形OABC的边OA=2,OC=6,在OC上取点D将△AOD沿AD翻折,使O点落在AB边上的E点处,将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动,且一直角边始终经过点D,另一直角边所在直线与直线DE,BC分别交于点M,N.
23. 校园安全与每个师生、家长和社会有着切身的关系.某校教学楼共五层,设有左、右两个楼梯口,通常在放学时,若持续不正常,会导致等待通过的人较多,发生拥堵,从而出现不安全因素.通过观察发现位于教学楼二、三楼的七年级学生从放学时刻起,经过单个楼梯口等待人数按每分钟12人递增,6分钟后经过单个楼梯口等待人数按每分钟12人递减;位于四、五楼的八年级学生从放学时刻起,经过单个楼梯口等待人数y2与时间为t(分)满足关系式y2=﹣4t2+48t﹣96(0≤t≤12).若在单个楼梯口等待人数超过80人,就会出现安全隐患.(1)、试写出七年级学生在单个楼梯口等待的人数y1(人)和从放学时刻起的时间t(分)之间的函数关系式,并指出t的取值范围.(2)、若七、八年级学生同时放学,试计算等待人数超过80人所持续的时间.(3)、为了避免出现安全隐患,该校采取让七年级学生提前放学措施,要使单个楼梯口等待人数不超过80人,则七年级学生至少比八年级提前几分钟放学?24. 如图,在平面直角坐标系中,矩形OABC的边OA=2,OC=6,在OC上取点D将△AOD沿AD翻折,使O点落在AB边上的E点处,将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动,且一直角边始终经过点D,另一直角边所在直线与直线DE,BC分别交于点M,N.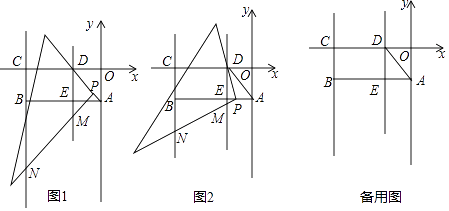 (1)、填空:经过A,B,D三点的抛物线的解析式是;(2)、已知点F在(1)中的抛物线的对称轴上,求点F到点B,D的距离之差的最大值;(3)、如图1,当点P在线段DA上移动时,是否存在这样的点M,使△CMN为等腰三角形?若存在,请求出M点坐标;若不存在,请说明理由;(4)、如图2,当点P在线段AB上移动时,设P点坐标为(x,﹣2),记△DBN的面积为S,请直接写出S与x之间的函数关系式,并求出S随x增大而增大时所对应的自变量x的取值范围.
(1)、填空:经过A,B,D三点的抛物线的解析式是;(2)、已知点F在(1)中的抛物线的对称轴上,求点F到点B,D的距离之差的最大值;(3)、如图1,当点P在线段DA上移动时,是否存在这样的点M,使△CMN为等腰三角形?若存在,请求出M点坐标;若不存在,请说明理由;(4)、如图2,当点P在线段AB上移动时,设P点坐标为(x,﹣2),记△DBN的面积为S,请直接写出S与x之间的函数关系式,并求出S随x增大而增大时所对应的自变量x的取值范围.