2017年湖北省黄冈市中考数学模拟试卷（c卷）

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

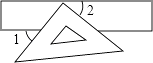
1. 计算（﹣20）+17的结果是（）

A、﹣3 B、3 C、﹣2017 D、2017

查看试题解析
2. 如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=48°，则∠2的度数为（）

A、48° B、42° C、40° D、45°

查看试题解析
3. “人间四月天，麻城看杜鹃”，2016年麻城市杜鹃花期间共接待游客约1200000人次，同比增长约26%，将1200000用科学记数法表示应是（）

A、12×10⁵ B、1.2×10⁶ C、1.2×10⁵ D、0.12×10⁵

查看试题解析
4. 下列各式变形中，正确的是（）

A、x²•x³=x⁶ B、 $\sqrt{x^{2}}$ =|x| C、（x²﹣ $\frac{1}{x}$ ）÷x=x﹣1 D、x²﹣x+1=（x﹣ $\frac{1}{2}$ ）²+ $\frac{1}{4}$

查看试题解析
5. 由若干个相同的小正方体组合而成的一个几何体的三视图如图所示，则组成这个几何体的小正方形个数是（）

A、3 B、4 C、5 D、6

查看试题解析
6. 麻城市思源实验学校篮球队12名队员的年龄如下表：
年龄：（岁）
13
14
15
16
人数
2
5
4
1
关于这12名队员的年龄，下列说法错误的是（）

A、众数是14 B、极差是3 C、中位数是14 D、平均数是14.8

查看试题解析

二、填空题

7. 某一天的最高气温为6℃，最低气温为﹣4℃，那么这天的最高气温比最低气温高℃

查看试题解析
8. 计算：|﹣2|+ $\sqrt[3]{- 8}$ +（π﹣3.14）⁰= ．

查看试题解析
9. 某班组织了一次读书活动，统计了16名同学在一周内的读书时间，他们一周内的读书时间累计如表，则这16名同学一周内累计读书时间的中位数是．
一周内累计的读书时间（小时）
5
8
10
14
人数（个）
1
7
5
3

查看试题解析
10. 如图，已知直线a∥b∥c，直线m交直线a，b，c于点A，B，C，直线n交直线a，b，c于点D，E，F，若 $\frac{A B}{B C} = \frac{1}{2}$ ，则 $\frac{D E}{D F}$ = ．

查看试题解析
11. 若关于x的方程 $\frac{x + m}{x - 3} + \frac{3 m}{3 - x}$ =3的解为非负数，则m的取值范围是．

查看试题解析
12. 从﹣3，﹣2，﹣1，0，1，3，4这七个数中随机抽取一个数记为a，a的值既是不等式组 ${\begin{matrix} 2 x + 3 < 4 \\ 3 x - 1 > - 11 \end{matrix}$ 的解，又在函数y= $\frac{1}{2 x^{2} + 2 x}$ 的自变量取值范围内的概率是．

查看试题解析
13. 如图，O为数轴原点，A，B两点分别对应﹣3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为．

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点C出发，按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒，当t为时，△ACP是等腰三角形．

查看试题解析

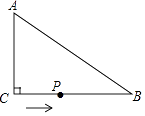
三、解答题

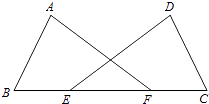
15. 先化简，再求值：（ $\frac{x^{2} - y}{x}$ ﹣x﹣1）÷ $\frac{x^{2} - y^{2}}{x^{2} - 2 x y + y^{2}}$ ，其中x= $\sqrt{5}$ ，y= $\sqrt{10}$ ．

查看试题解析
16. 如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．

查看试题解析
17. 已知关于x的方程x²+ax+a﹣2=0．

(1)、若该方程的一个根为2，求a的值及该方程的另一根．

(2)、求证：不论a取何实数，该方程都有两个不相等的实数根．

查看试题解析
18. 有甲、乙、丙三种糖果混合而成的什锦糖100千克，其中各种糖果的单价和千克数如表所示，商家用加权平均数来确定什锦糖的单价．
甲种糖果
乙种糖果
丙种糖果
单价（元/千克）
20
25
30
千克数
40
40
20

(1)、求该什锦糖的单价．

(2)、为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中加入甲、丙两种糖果共100千克，问其中最多可加入丙种糖果多少千克？

查看试题解析
19. 每年5月的第二周为：“职业教育活动周”，今年我市展开了以“弘扬工匠精神，打造技能强国”为主题的系列活动，活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动，相关职业技术人员进行了现场演示，活动后该校随机抽取了部分学生进行调查：“你最感兴趣的一种职业技能是什么？”并对此进行了统计，绘制了统计图（均不完整）．

(1)、补全条形统计图和扇形统计图；

(2)、若该校共有3000名学生，请估计该校对“工艺设计”最感兴趣的学生有多少人？

(3)、要从这些被调查的学生中随机抽取一人进行访谈，那么正好抽到对“机电维修”最感兴趣的学生的概率是．

查看试题解析
20. 如图，已知⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．

(1)、求证：DE是⊙O的切线．

(2)、求DE的长．

查看试题解析
21. 如图，点A为函数 $y = \frac{18}{x} (x > 0)$ 图象上一点，连结OA，交函数 $y = \frac{2}{x} (x > 0)$ 的图象于点B，点C是x轴上一点，且AO=AC，求△ABC的面积．

查看试题解析
22. 如图，书桌上的一种新型台历和一块主板AB、一个架板AC和环扣（不计宽度，记为点A）组成，其侧面示意图为△ABC，测得AC⊥BC，AB=5cm，AC=4cm，现为了书写记事方便，须调整台历的摆放，移动点C至C′，当∠C′=30°时，求移动的距离即CC′的长（或用计算器计算，结果取整数，其中 $\sqrt{3}$ =1.732， $\sqrt{21}$ =4.583）

查看试题解析
23. 麻城市思源实验学校自从开展“高效课堂”模式以来，在课堂上进行当堂检测效果很好．每节课40分钟教学，假设老师用于精讲的时间x（单位：分钟）与学生学习收益量y的关系如图1所示，学生用于当堂检测的时间x（单位：分钟）与学生学习收益y的关系如图2所示（其中OA是抛物线的一部分，A为抛物线的顶点），且用于当堂检测的时间不超过用于精讲的时间．

(1)、求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式；

(2)、求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式；

(3)、问此“高效课堂”模式如何分配精讲和当堂检测的时间，才能使学生在这40分钟的学习收益总量最大？

查看试题解析
24.
如图，Rt△OAB如图所示放置在平面直角坐标系中，直角边OA与x轴重合，∠OAB=90°，OA=4，AB=2，把Rt△OAB绕点O逆时针旋转90°，点B旋转到点C的位置，一条抛物线正好经过点O，C，A三点．

(1)、求该抛物线的解析式；

(2)、在x轴上方的抛物线上有一动点P，过点P作x轴的平行线交抛物线于点M，分别过点P，点M作x轴的垂线，交x轴于E，F两点，问：四边形PEFM的周长是否有最大值？如果有，请求出最值，并写出解答过程；如果没有，请说明理由．

(3)、如果x轴上有一动点H，在抛物线上是否存在点N，使O（原点）、C、H、N四点构成以OC为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．

查看试题解析

一周内累计的读书时间（小时）	5	8	10	14
人数（个）	1	7	5	3

	甲种糖果	乙种糖果	丙种糖果
单价（元/千克）	20	25	30
千克数	40	40	20

年龄：（岁）	13	14	15	16
人数	2	5	4	1