2017年河南省周口市商水县中考数学二模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 在实数0,﹣π, ,﹣4中,最小的数是( )A、0 B、﹣π C、 D、﹣42. 若不等式组 有解,则a的取值范围是( )A、a≤3 B、a<3 C、a<2 D、a≤23. 我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为5500万千米,这个数据用科学记数法可表示为( )
 A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
A、5.5×106千米 B、5.5×107千米 C、55×106千米 D、0.55×108千米4. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、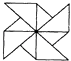 B、
B、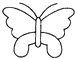 C、
C、 D、
D、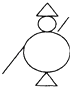 5. 下列计算正确的是( )A、m2•m4=m8 B、(﹣m3)2=m5 C、m0=1 D、(﹣m2)3=﹣m66. 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
5. 下列计算正确的是( )A、m2•m4=m8 B、(﹣m3)2=m5 C、m0=1 D、(﹣m2)3=﹣m66. 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( ) A、40° B、50° C、80° D、100°7. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
A、40° B、50° C、80° D、100°7. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )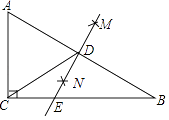 A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC8. 关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m≥﹣ B、m≤﹣ C、m<﹣ D、m>﹣9.
A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC8. 关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m≥﹣ B、m≤﹣ C、m<﹣ D、m>﹣9.如图,已知抛物线y=x2+2x﹣3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(﹣2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( )
10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) A、( )2016 B、( )2017 C、( )2016 D、( )2017
A、( )2016 B、( )2017 C、( )2016 D、( )2017二、填空题
-
11. 分解因式:(a﹣b)2﹣4b2= .12. 在一个不透明的盒子中装有16个白球,若干个黄球,它们除了颜色不同外,其余均相同,若从中随机摸出一个球是黄球的概率是 ,则黄球的个数为 .13. 如图所示,点A在双曲线y= 上,点A的坐标是( ,2),点B在双曲线y= 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
 14. 如图,正方形ABCD的面积为36cm2 , 点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画 ,连接AF,CF,则图中阴影部分的面积为 .
14. 如图,正方形ABCD的面积为36cm2 , 点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画 ,连接AF,CF,则图中阴影部分的面积为 . 15. 如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 .
15. 如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 .
三、解答题
-
16. 先化简,再求值: ,其中x=3tan30°+1.17. 如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
 (1)、求证:△CDF≌△BDE;(2)、当AD=时,四边形AODC是菱形;(3)、当AD=时,四边形AEDF是正方形.18. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)、求证:△CDF≌△BDE;(2)、当AD=时,四边形AODC是菱形;(3)、当AD=时,四边形AEDF是正方形.18. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: (1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.19.
(1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.19.如图,一楼房AB后有一假山,其坡度为i=1: ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
 20. 随着纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也逐步增大.某商场从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7 500元购进A型空气净化器和用6 000元购进B型空气净化器的台数相同.(1)、求一台A型空气净化器和一台B型空气净化器的进价各为多少元?(2)、经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商场销售B型空气净化器的利润为3200元,请问该商场应将B型空气净化器的售价定为多少元?(3)、已知A型空气净化器净化能力为340m3/h,B型空气净化器净化能力为240m3/h.某公司室内办公场地总面积为600m2 , 室内墙高3.5m.受二胎政策影响,近期孕妇数量激增,为保证胎儿健康成长,该公司计划购买15台空气净化器净化空气,每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,该公司至少要购买A型空气净化器多少台?21. 数学李老师给学生出了这样一个问题:探究函数y= 的图象与性质,小斌根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
20. 随着纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也逐步增大.某商场从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7 500元购进A型空气净化器和用6 000元购进B型空气净化器的台数相同.(1)、求一台A型空气净化器和一台B型空气净化器的进价各为多少元?(2)、经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商场销售B型空气净化器的利润为3200元,请问该商场应将B型空气净化器的售价定为多少元?(3)、已知A型空气净化器净化能力为340m3/h,B型空气净化器净化能力为240m3/h.某公司室内办公场地总面积为600m2 , 室内墙高3.5m.受二胎政策影响,近期孕妇数量激增,为保证胎儿健康成长,该公司计划购买15台空气净化器净化空气,每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,该公司至少要购买A型空气净化器多少台?21. 数学李老师给学生出了这样一个问题:探究函数y= 的图象与性质,小斌根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成: (1)、函数y= 的自变量x的取值范围是:(2)、列出y与x的几组对应值,请直接写出m的值,m= .
(1)、函数y= 的自变量x的取值范围是:(2)、列出y与x的几组对应值,请直接写出m的值,m= .x
…
﹣5
﹣4
﹣3
﹣2
﹣
﹣
0
1
2
m
4
5
…
y
…
2
3
﹣1
0
…
(3)、请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;(4)、结合函数的图象,写出函数y= 的一条性质.22. 探究题(1)、探究发现:
下面是一道例题及其解答过程,请补充完整:
如图①在等边△ABC内部,有一点P,若∠APB=150°.求证:AP2+BP2=CP2

证明:将△APC绕A点逆时针旋转60°,得到△AP′B,连接PP′,则△APP′为等边三角形
∴∠APP′=60° PA=PP′PC=
∵∠APB=150°∴∠BPP′=90°
∴P′P2+BP2=
即PA2+PB2=PC2
(2)、类比延伸:
如图②在等腰三角形ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA、PB、PC之间的数量关系,并证明.
 (3)、
(3)、联想拓展:
如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2 , 请直接写出k的值.
 23.
23.如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
 (1)、求二次函数的关系式;(2)、点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;(3)、在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
(1)、求二次函数的关系式;(2)、点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;(3)、在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.