2017年河南省许昌市中考数学二模试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、选择题
-
1. ﹣2的倒数是（ ）A、2 B、 C、﹣2 D、﹣2. 已知一个几何体的三种视图如图所示，则这个几何体是（ ）
A、圆柱 B、圆锥 C、球体 D、正方体3. 下列运算中，结果正确的是（ ）A、（a3）2=a6 B、（ab）3=a3b C、a•a3=a3 D、a8÷a4=a24. 如图，直线m∥n，∠1=70°，∠2=30°，则∠A等于（ ）
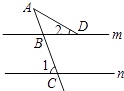A、30° B、35° C、40° D、50°5. 估算 的值在（ ）A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 如图，在▱ABCD中，E为AD的三等分点，AE= AD，连接BE交AC于点F，AC=12，则AF为（ ）
A、4 B、4.8 C、5.2 D、67. 星期天，小明从家出发，以15千米/小时的速度骑车去郊游，到达目的地休息一段时间后原路返回，已知小明行驶的路程s（千米）与时间t（小时）之间的函数关系如图所示，则小明返程的速度为（ ）
A、15千米/小时 B、10千米/小时 C、6千米/小时 D、无法确定8. 如图，AB是半圆O的直径，C是半圆O上一点，CD是⊙O的切线，OD∥BC，OD与半圆O交于点E，则下列结论中不一定正确的是（ ）
A、AC⊥BC B、BE平分∠ABC C、BE∥CD D、∠D=∠A二、填空题
-
9. 计算：2﹣2﹣ = ．10. 写出一个二次函数解析式，使它的图象的顶点在y轴上： ．11. 课外活动中，九（1）班准备把全班男生随机分成两个小组进行拔河比赛，则甲、乙、丙三位同学恰好被分在同一小组的概率为 ．12. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以点A为圆心，AC的长为半径作 交AB于点E，以点B为圆心，BC的长为半径作 交AB于点D，则阴影部分的面积为 ．
13. 如图，矩形ABCD中，AB=8，BC=15，点E是AD边上一点，连接BE，把△ABE沿BE折叠，使点A落在点A′处，点F是CD边上一点，连接EF，把△DEF沿EF折叠，使点D落在直线EA′上的点D′处，当点D′落在BC边上时，AE的长为 ．
三、解答题
-
14. 先化简，再求值：（ ﹣ ）÷ ，其中实数a，b满足（a﹣2）2+|b﹣2a|=0．15. 每年的3月22日为联合国确定的“世界水日”，某社区为了宣传节约用水，从本社区1000户家庭中随机抽取部分家庭，调查他们每月的用水量，并将调查的结果绘制成如下两幅尚不完整的统计图（每组数据包括右端点但不包括左端点），请你根据统计图解答下列问题：
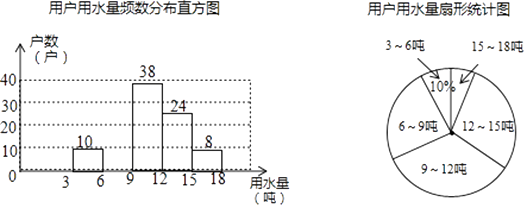(1)、此次抽样调查的样本容量是；(2)、补全频数分布直方图，求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数；(3)、如果自来水公司将基本月用水量定为每户每月12吨，不超过基本月用水量的部分享受基本价格，超出基本月用水量的部分实行加价收费，那么该社会用户中约有多少户家庭能够全部享受基本价格？16. 如图，△ABC是半径为2的⊙O的内接三角形，连接OA、OB，点D、E、F、G分别是CA、OA、OB、CB的中点．
(1)、试判断四边形DEFG的形状，并说明理由；(2)、填空：①若AB=3，当CA=CB时，四边形DEFG的面积是；
②若AB=2，当∠CAB的度数为时，四边形DEFG是正方形．
17.某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的北岸边点A处，测得河的南岸边点B在其南偏东45°方向，然后向北走20米到达C点，测得点B在点C的南偏东33°方向，求出这段河的宽度（结果精确到1米，参考数据sin33°≈0.54，cos33°≈0.84，tan33°≈0.65， ≈1.41）
18. 如图，直线y=﹣x+b与反比例函数y= 的图形交于A（a，4）和B（4，1）两点．
(1)、求b，k的值；(2)、在第一象限内，当一次函数y=﹣x+b的值大于反比例函数y= 的值时，直接写出自变量x的取值范围；(3)、将直线y=﹣x+b向下平移m个单位，当直线与双曲线只有一个交点时，求m的值．19. 某化工材料经销公司购进一种化工原料若干千克，物价部门规定其销售单价不低于进价，不高于60元/千克，经市场调查发现：销售单价定为60元/千克时，每日销售20千克；如调整价格，每降价1元/千克，每日可多销售2千克．(1)、已知某天售出该化工原料40千克，则当天的销售单价为 50 元/千克；(2)、该公司现有员工2名，每天支付员工的工资为每人每天90元，每天应支付其他费用108元，当某天的销售价为46元/千克时，收支恰好平衡．①求这种化工原料的进价；
②若公司每天的纯利润（收入﹣支出）全部用来偿还一笔10000元的借款，则至少需多少天才能还清借款？
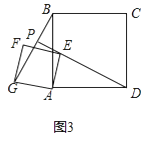
20.如图1，四边形ABCD是正方形，点E是AB边的中点，以AE为边作正方形AEFG，连接DE，BG．
(1)、发现①线段DE、BG之间的数量关系是；
②直线DE、BG之间的位置关系是 ．
(2)、探究
如图2，将正方形AEFG绕点A逆时针旋转，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
(3)、应用
如图3，将正方形AEFG绕点A逆时针旋转一周，记直线DE与BG的交点为P，若AB=4，请直接写出点P到CD所在直线距离的最大值和最小值．
21.如图，以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A，点B（﹣1，0），与y轴交于点C（0，4），作直线AC．
(1)、求抛物线解析式；(2)、点P在抛物线的对称轴上，且到直线AC和x轴的距离相等，设点P的纵坐标为m，求m的值；(3)、点M在y轴上且位于点C上方，点N在直线AC上，点Q为第一象限内抛物线上一点，若以点C、M、N、Q为顶点的四边形是菱形，请直接写出点Q的坐标．