2017年湖南省衡阳市中考数学一模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 在实数0，π， $\frac{22}{7}$ ， $\sqrt{2}$ ， $- \sqrt{9}$ 中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 数据﹣0.00000012用科学记数法表示正确的是（）

A、1.2×10⁷ B、﹣1.2×10^﹣⁷ C、1.2×10⁸ D、﹣1.2×10⁸

查看试题解析
3. 把1枚质地均匀的普通硬币重复掷两次，落地后出现一次正面一次反面的概率是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
4. 如图，已知直线AB∥CD，直线l与直线AB、CD相交于点，E、F，将l绕点E逆时针旋转40°后，与直线AB相交于点G，若∠GEC=80°，那么∠GFE=（）

A、60° B、50° C、40° D、30°

查看试题解析
5. 如图是由一些相同的小正方体构成的几何体的三视图，则构成构成这个几何体的小正方体的个数是（）

A、3 B、4 C、5 D、6

查看试题解析
6. 函数y= $\sqrt{2 x - 1}$ 中自变量x的取值范围是（）

A、x≥﹣ $\frac{1}{2}$ B、x≥ $\frac{1}{2}$ C、x≤﹣ $\frac{1}{2}$ D、x≤ $\frac{1}{2}$

查看试题解析
7. 下列计算正确的是（　　）

A、a²•a³=a⁶ B、2a+3b=5ab C、a⁸÷a²=a⁶ D、（a²b）²=a⁴b

查看试题解析
8. 下列长度的三条线段能组成三角形的是（）

A、3，2，1 B、3，2，5 C、3，4，6 D、3，4，7

查看试题解析
9. 下列命题为真命题的是（）

A、若a²=b² ，则a=b B、等角的补角相等 C、b边形的外角和为（n﹣2）=180° D、若 $\bar{x_{乙}}$ = $\bar{x_{甲}}$ ，S $_{甲}^{2}$ ＞S $_{乙}^{2}$ ，则甲数据更稳定

查看试题解析
10. 如图，四边形ABCD内接于⊙O，已知∠ADC=130°，则∠AOC的大小是（）

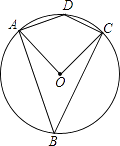A、80° B、100° C、60° D、40°

查看试题解析
11. 施工队要铺设一段全长2000米的管道，因在中考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则根据题意所列方程正确的是（）

A、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x + 50}$ =2 B、 $\frac{2000}{x + 50}$ ﹣ $\frac{2000}{x}$ =2 C、 $\frac{2000}{x}$ ﹣ $\frac{2000}{x - 50}$ =2 D、 $\frac{2000}{x - 50}$ ﹣ $\frac{2000}{x}$ =2

查看试题解析
12. 如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题

13. 分解因式：x³﹣4x= ．

查看试题解析
14. 分式 $\frac{1}{x - 1}$ 有意义的条件是．

查看试题解析
15. 把半径为4cm的半圆围成一个圆锥，则圆锥的底面圆半径为．

查看试题解析
16. 已知x﹣ $\frac{1}{x}$ =4，则x²﹣4x+5的值为．

查看试题解析
17. 在平行四边形ABCD中，点O是对角线AC、BD的交点，AC⊥BC，且AB=10cm，AD=6cm，则AO=cm．

查看试题解析
18.
如图，在平面直角坐标系中，直线l：y= $\frac{\sqrt{3}}{3}$ x，点A₁（0，1），过点A₁作y轴的垂线交直线l于点B₁ ，以原点O为圆心，OB₁长为半径画弧交y轴于点A₂；再过点A₂作y轴的垂线交直线l于点B₂ ，以原点O为圆心，OB₂长为半径画弧交y轴于点A₃ ， …，按此作法进行下去，则OA₂₀₁₇= ．

查看试题解析

三、解答题

19. 计算：|﹣2|﹣2cos60°+（ $\frac{1}{6}$ ）^﹣¹﹣（π﹣ $\sqrt{3}$ ）⁰ ．

查看试题解析
20. 先化简，再求值：x（x﹣2）﹣（x+1）² ，其中x=1．

查看试题解析
21. 解不等式组： ${\begin{matrix} 2 x - 1 > \frac{3 x - 1}{2} \\ 2 x + 1 \geq 0 \end{matrix}$ ，并把解集表示在数轴上．

查看试题解析
22. 如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：∠B=∠E．

查看试题解析
23. 一个不透明的口袋里装有红、黄、绿三种颜色的球（除颜色不同外其余都相同），其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为 $\frac{1}{2}$ ．

(1)、试求袋中绿球的个数；

(2)、第1次从袋中任意摸出1球（不放回），第2次再任意摸出1球，请你用画树状图或列表格的方法，求两次都摸到红球的概率．

查看试题解析
24. 某班组织班团活动，班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品，已知笔记本2元/本，中性笔1元/支，且每种奖品至少买1件．

(1)、若设购买笔记本x本，中性笔y支，写出y与x之间的关系式；

(2)、有多少种购买方案？请列举所有可能的结果；

(3)、从上述方案中任选一种方案购买，求买到的中性笔与笔记本数量相等的概率．

查看试题解析
25. 如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．

(1)、求证：AC平分∠DAB；

(2)、连接BE交AC于点F，若cos∠CAD= $\frac{4}{5}$ ，求 $\frac{A F}{F C}$ 的值．

查看试题解析
26.
如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：

(1)、求点N的坐标（用含x的代数式表示）；

(2)、设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？

(3)、在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．

查看试题解析
27.
如图，抛物线y=﹣ $\frac{1}{4}$ x²+mx+n的图象经过点A（2，3），对称轴为直线x=1，一次函数y=kx+b的图象经过点A，交x轴于点P，交抛物线于另一点B，点A、B位于点P的同侧．

(1)、求抛物线的解析式；

(2)、若PA：PB=3：1，求一次函数的解析式；

(3)、在（2）的条件下，当k＞0时，抛物线的对称轴上是否存在点C，使得⊙C同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在，请说明理由．

查看试题解析