2017年河南省商丘市柘城县中考数学四模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 2的相反数是（）

A、2 B、﹣2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. x²•x³=（）

A、x⁵ B、x⁶ C、x⁸ D、x⁹

查看试题解析
3. 如图，有6张扑克牌，从中随机抽取一张，点数为偶数的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图是由6个大小相同的小正方体组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
5. 正方形的对称轴的条数为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 下列命题中，假命题是（）

A、对顶角相等 B、三角形两边的和小于第三边 C、菱形的四条边都相等 D、多边形的外角和等于360°

查看试题解析
7. 若（m﹣1）²+ $\sqrt{n + 2}$ =0，则m+n的值是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
8. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同．设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（）

A、 $\frac{600}{x + 50}$ = $\frac{450}{x}$ B、 $\frac{600}{x - 50}$ = $\frac{450}{x}$ C、 $\frac{600}{x}$ = $\frac{450}{x + 50}$ D、 $\frac{600}{x}$ = $\frac{450}{x - 50}$

查看试题解析
9.
如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（）

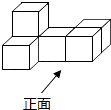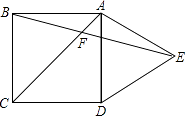A、45° B、55° C、60° D、75°

查看试题解析
10.
如图，Rt△ABC中，AC=BC=2，正方形CDEF的顶点D、F分别在AC、BC边上，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 据统计，2014年全国约有939万人参加高考，939万人用科学记数法表示为
人．

查看试题解析
12. 已知一组数据：6，6，6，6，6，6，则这组数据的方差为．
【注：计算方差的公式是S²= $\frac{1}{n}$ [（x₁﹣ $\bar{x}$ ）²+（x₂﹣ $\bar{x}$ ）²+…+（x_n﹣ $\bar{x}$ ）²]】

查看试题解析
13. 已知：m、n为两个连续的整数，且m＜ $\sqrt{11}$ ＜n，则m+n= ．

查看试题解析
14. 如图，有一直径是 $\sqrt{2}$ 米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：

(1)、AB的长为米；

(2)、用该扇形铁皮围成一个圆锥，所得圆锥的底面圆的半径为米．

查看试题解析
15.
如图放置的△OAB₁ ， △B₁A₁B₂ ， △B₂A₂B₃ ， …都是边长为2的等边三角形，边AO在y轴上，点B₁ ， B₂ ， B₃ ， …都在直线y= $\frac{\sqrt{3}}{3}$ x上，则A₂₀₁₄的坐标是．

查看试题解析

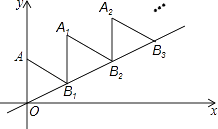
三、解答题

16. 先化简 $(\frac{x^{2} - 4}{x^{2} - 4 x + 4} - \frac{1}{2 - x}) \div \frac{1}{x^{2} - 2 x}$ ，再在0，﹣1，2中选取一个适当的数代入求值．

查看试题解析
17. 如图，以△ABC的BC边上一点O为圆心，经过A，C两点且与BC边交于点E，点D为CE的下半圆弧的中点，连接AD交线段EO于点F，若AB=BF．

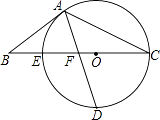(1)、求证：AB是⊙O的切线；

(2)、若CF=4，DF= $\sqrt{10}$ ，求⊙O的半径r及sinB．

查看试题解析
18. 某校初三（1）班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题．

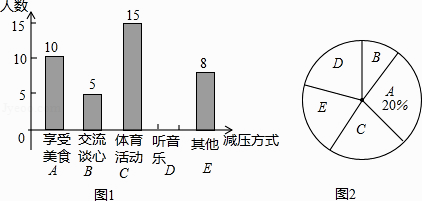(1)、初三（1）班接受调查的同学共有多少名；

(2)、补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数；

(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生；老师想从5名同学中任选两名同学进行交流，直接写出选取的两名同学都是女生的概率．

查看试题解析
19. 为倡导“低碳生活”，人们常选择以自行车作为代步工具、图（1）所示的是一辆自行车的实物图．图（2）是这辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45cm和60cm，且它们互相垂直，座杆CE的长为20cm．点A、C、E在同一条直线上，且∠CAB=75°．（参考数据：sin75°=0.966，cos75°=0.259，tan75°=3.732）

(1)、求车架档AD的长；

(2)、求车座点E到车架档AB的距离（结果精确到1cm）．

查看试题解析
20. 如图，在直角坐标系xOy中，直线y=mx与双曲线 $y = \frac{n}{x}$ 相交于A（﹣1，a）、B两点，BC⊥x轴，垂足为C，△AOC的面积是1．

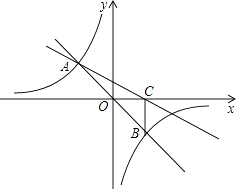(1)、求m、n的值；

(2)、求直线AC的解析式．

查看试题解析
21. 杨梅是漳州的特色时令水果，杨梅一上市，水果店的老板用1200元购进一批杨梅，很快售完；老板又用2500元购进第二批杨梅，所购件数是第一批的2倍，但进价比第一批每件多了5元．

(1)、第一批杨梅每件进价多少元？

(2)、老板以每件150元的价格销售第二批杨梅，售出80%后，为了尽快售完，决定打折促销，要使第二批杨梅的销售利润不少于320元，剩余的杨梅每件售价至少打几折？（利润=售价﹣进价）

查看试题解析
22.
如图1，在菱形ABCD中，对角线AC与BD相交于点O，AB=13，BD=24，在菱形ABCD的外部以AB为边作等边三角形 ABE．点F是对角线BD上一动点（点F不与点B重合），将线段AF绕点A顺时针方向旋转60°得到线段AM，连接FM．

(1)、求AO的长；

(2)、
如图2，当点F在线段BO上，且点M，F，C三点在同一条直线上时，求证：AC= $\sqrt{3}$ AM；

(3)、连接EM，若△AEM的面积为40，请直接写出△AFM的周长．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答

查看试题解析
23.
如图，抛物线y=x²+bx+c与直线y= $\frac{1}{2}$ x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．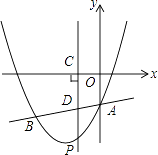

(1)、求抛物线的解析式；

(2)、以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．

(3)、当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．

查看试题解析