2017年湖南省衡阳市中考数学模拟试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. ﹣2的倒数是( )A、 B、﹣ C、2 D、﹣22. 在3,﹣1,0,﹣2这四个数中,最大的数是( )A、0 B、6 C、﹣2 D、33. 右图是由4个相同的小正方体组成的几何体,其俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、( )﹣2=9 B、 =﹣2 C、(﹣2)0=﹣1 D、|﹣5﹣3|=25. 下列运算中,计算正确的是( )A、2a•3a=6a B、(3a2)3=27a6 C、a4÷a2=2a D、(a+b)2=a2+ab+b26. 不等式组 的解集在数轴上表示为( )A、
4. 下列计算正确的是( )A、( )﹣2=9 B、 =﹣2 C、(﹣2)0=﹣1 D、|﹣5﹣3|=25. 下列运算中,计算正确的是( )A、2a•3a=6a B、(3a2)3=27a6 C、a4÷a2=2a D、(a+b)2=a2+ab+b26. 不等式组 的解集在数轴上表示为( )A、 B、
B、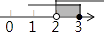 C、
C、 D、
D、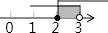 7. 内角为108°的正多边形是( )A、3 B、4 C、5 D、68. 将直线y=﹣2x向下平移两个单位,所得到的直线为( )A、y=﹣2(x+2) B、y=﹣2(x﹣2) C、y=﹣2x﹣2 D、y=﹣2x+29. 已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )A、11 B、5 C、2 D、110. 如图,函数y=﹣2x2 的图象是( )
7. 内角为108°的正多边形是( )A、3 B、4 C、5 D、68. 将直线y=﹣2x向下平移两个单位,所得到的直线为( )A、y=﹣2(x+2) B、y=﹣2(x﹣2) C、y=﹣2x﹣2 D、y=﹣2x+29. 已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )A、11 B、5 C、2 D、110. 如图,函数y=﹣2x2 的图象是( ) A、① B、② C、③ D、④11. 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
A、① B、② C、③ D、④11. 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( ) A、
A、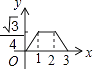 B、
B、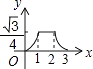 C、
C、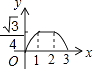 D、
D、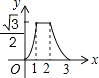
二、填空题
-
12. 某工厂去年的产值是a万元,今年比去年增加10%,今年的产值是万元.13. 数据:3、5、4、5、2、3、4的中位数是 .14. + = .15. 如图所示,在▱ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为 .
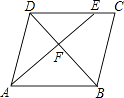 16. 如图,⊙O的半径为5,点P是弦AB延长线上的一点,连接OP,若OP=8,∠P=30°,则弦AB的长为 .
16. 如图,⊙O的半径为5,点P是弦AB延长线上的一点,连接OP,若OP=8,∠P=30°,则弦AB的长为 .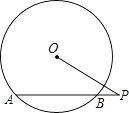 17. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为 .
17. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为 .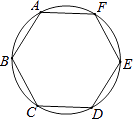
三、解答题
-
18. 化简: .19. 如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
 20. 关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1 , x2 .(1)、求m的取值范围;(2)、若2(x1+x2)+x1x2+10=0,求m的值.21. 松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
20. 关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1 , x2 .(1)、求m的取值范围;(2)、若2(x1+x2)+x1x2+10=0,求m的值.21. 松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图: (1)、求C型号种子的发芽数;(2)、通过计算说明,应选哪种型号的种子进行推广?(3)、如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.22. 如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)、求C型号种子的发芽数;(2)、通过计算说明,应选哪种型号的种子进行推广?(3)、如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.22. 如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC. (1)、山坡坡角(即∠ABC)的度数等于度;(2)、求山坡A、B两点间的距离(结果精确到0.1米).
(1)、山坡坡角(即∠ABC)的度数等于度;(2)、求山坡A、B两点间的距离(结果精确到0.1米).(参考数据: ≈1.414, ≈1.732)
23. 某装修工程,甲、乙两人可以合作完成,若甲、乙两人合作4天后,再由乙独作12天可以完成,已知甲独作每天需要费用580元.乙独作每天需费用280元.但乙单独完成的天数是甲单独完成天数的2倍.(1)、甲、乙两人单独作这项工程各需多少天?(2)、如果工期要求不超过18天完成,应如何安排甲乙两人的工期使这项工程比较省钱?24. 如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.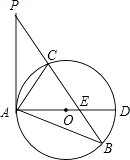 (1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长.25. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.
(1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长.25. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点. (1)、证明四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、已知在y= 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.26. 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
(1)、证明四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、已知在y= 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.26. 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.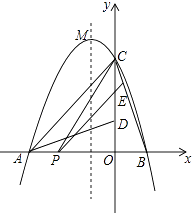 (1)、求该二次函数的解析式;(2)、若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;(3)、设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
(1)、求该二次函数的解析式;(2)、若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;(3)、设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.