2017年湖北省孝感市安陆市中考数学模拟试卷（5月份）

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是（）

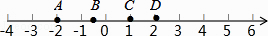A、点A B、点B C、点C D、点D

查看试题解析
2. 2017年4月20日，天舟一号货运飞船在我国文昌航天发射场发射成功，进入距离地球393000米的预定轨道，将393000用科学记数法表示应为（）

A、0.393×10⁷ B、3.93×10⁵ C、3.93×10⁶ D、393×10³

查看试题解析
3. 某物体的三视图如图，那么该物体形状可能是（）

A、长方体 B、圆锥 C、正方体 D、圆柱

查看试题解析
4. 《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）

A、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 ${\begin{matrix} y - 8 x = 3 \\ y - 7 x = 4 \end{matrix}$ D、 ${\begin{matrix} 8 x - y = 3 \\ 7 x - y = 4 \end{matrix}$

查看试题解析
5. 如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于（）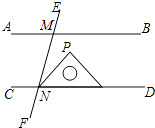

A、15° B、25° C、30° D、45°

查看试题解析
6. 在平面直角坐标系中，点P（﹣3，2）关于直线y=x对称点的坐标是（）

A、（﹣3，﹣2） B、（3，2） C、（2，﹣3） D、（3，﹣2）

查看试题解析
7. 某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：
年龄（单位：岁）
13
14
15
16
频数（单位：名）
5
15
x
10﹣x
对于不同的x，下列关于年龄的统计量不会发生改变的是（）

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

查看试题解析
8. 某商店在节日期间开展优惠促销活动：购买原价超过200元的商品，超过200元的部分可以享受打折优惠．若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）的函数关系的图象如图所示，则超过200元的部分可以享受的优惠是（）

A、打八折 B、打七折 C、打六折 D、打五折

查看试题解析
9. 如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
10.
如图所示，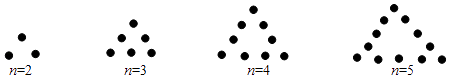
将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为a_n ，则 $\frac{9}{a_{2} a_{3}}$ + $\frac{9}{a_{3} a_{4}}$ +…+ $\frac{9}{a_{2017} a_{2018}}$ =（）

A、 $\frac{2015}{2016}$ B、 $\frac{2016}{2017}$ C、 $\frac{2017}{2018}$ D、 $\frac{2018}{2017}$

查看试题解析

二、填空题

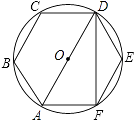
11. 方程x²﹣2=0的根是．

查看试题解析
12. 某坡面的坡度是 $\sqrt{3}$ ：1，则坡角α是度．

查看试题解析
13. 如图所示，正六边形ABCDEF内接于⊙O，则∠ADF的度数为．

查看试题解析
14. 一只不透明的袋子中装有红球和白球共30个，这些球除了颜色外都相同，校课外学习小组做摸球试验，将球搅匀后任意摸出一个球，记下颜色后放回、搅匀，通过多次重复试验，算得摸到红球的频率是20%，则袋中有个红球．

查看试题解析
15. 如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为．

查看试题解析
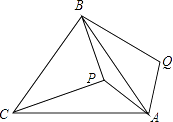16. 已知二次函数y=ax²+bx+c的图象如图所示，给出下列结论：①abc＞0；②a﹣b+c＜0；③2a+b﹣c＜0；④4a+2b+c＞0，⑤若点（﹣ $\frac{2}{3}$ ，y₁）和（ $\frac{7}{3}$ ，y₂）在该图象上，则y₁＞y₂ ．其中正确的结论是（填入正确结论的序号）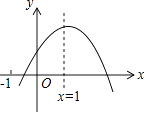

查看试题解析

三、解答题

17. 综合题。

(1)、（﹣2）^﹣¹﹣|﹣ $\sqrt{8}$ |+（3.14﹣π）⁰+4cos45°

(2)、已知x²﹣2x﹣7=0，求（x﹣2）²+（x+3）（x﹣3）的值．

查看试题解析
18. 解方程： $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$ ．

查看试题解析
19. 某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
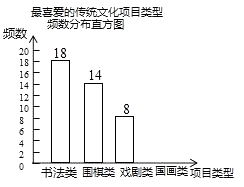
根据以上信息完成下列问题：

(1)、频数分布表中a= ， b=；

(2)、补全频数分布直方图；

(3)、若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？

查看试题解析
20. 去学校食堂就餐，经常会在一个买菜窗口前等待，经调查发现，同学的舒适度指数y与等时间x（分）之间满足反比例函数关系，如下表：
等待时间x
1
2
5
10
20
舒适度指数y
100
50
20
10
5
已知学生等待时间不超过30分钟

(1)、求y与x的函数关系式，并写出自变量x的取值范围．

(2)、若等待时间8分钟时，求舒适度的值；

(3)、舒适度指数不低于10时，同学才会感到舒适．请说明，作为食堂的管理员，让每个在窗口买菜的同学最多等待多少时间？

查看试题解析
21. 已知关于x的方程x²﹣（m+2）x+2m﹣1=0．

(1)、求证：此方程有两个不相等的实数根；

(2)、若抛物线y=x²﹣（m+2）x+2m﹣1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；

(3)、填空：若x²﹣（m+2）x+2m﹣1=0的两根都大于1，则m的取值范围是．

查看试题解析
22. 如图，在平面直角坐标系中，⊙P经过y轴上一点C，与x轴分别相交于A、B两点，连接BP并延长分别交⊙P、y轴于点D、E，连接DC并延长交x轴于点F．若点F的坐标为（﹣1，0），点D的坐标为（1，6）．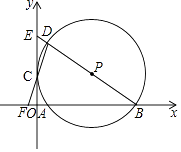

(1)、求证：CD=CF；

(2)、判断⊙P与y轴的位置关系，并说明理由；

(3)、求直线BD的解析式．

查看试题解析
23. 在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．

(1)、
若点D在线段BC上，如图1．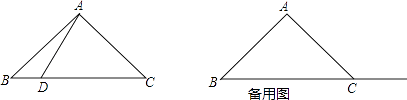
①依题意补全图1；
②判断BC与CG的数量关系与位置关系，并加以证明；

(2)、若点D在线段BC的延长线上，且G为CF中点，连接GE，AB= $\sqrt{2}$ ，则GE的长为 $\underline{}$ ，并简述求GE长的思路．

查看试题解析
24.
如图，直线l：y=x﹣ $\sqrt{3}$ 与x轴正半轴、y轴负半轴分别相交于A、C两点，抛物线y= $\frac{\sqrt{3}}{3}$ x²+bx+c经过点B（﹣1，0）和点C．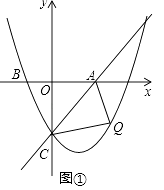

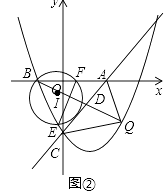
(1)、填空：直接写出抛物线的解析式：；

(2)、已知点Q是抛物线y= $\frac{\sqrt{3}}{3}$ x²+bx+c在第四象限内的一个动点．
①如图，连接AQ、CQ，设点Q的横坐标为t，△AQC的面积为S，求S与t的函数关系式，并求出S的最大值；
②连接BQ交AC于点D，连接BC，以BD为直径作⊙I，分别交BC、AB于点E、F，连接EF，求线段EF的最小值，并直接写出此时Q点的坐标．

查看试题解析

年龄（单位：岁）	13	14	15	16
频数（单位：名）	5	15	x	10﹣x

项目类型	频数	频率
书法类	18	a
围棋类	14	0.28
喜剧类	8	0.16
国画类	b	0.20

等待时间x	1	2	5	10	20
舒适度指数y	100	50	20	10	5