2017年河南省濮阳市中考数学模拟试卷（5月份）

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，比﹣2小的是（）

A、﹣1 B、﹣3 C、0 D、 $\frac{π}{2}$

查看试题解析
2. 雾霾天气给人们的健康带来严重危害．教生物的李老师通过显微镜，将空气中细小的霾颗粒放大1000倍，发现这些霾颗粒平均直径为15微米〜25微米，其中25微米（1微米=0.000001米）用科学记数法可表示为（）

A、2.5×10⁶ B、2.5×10⁵ C、2.5×10^﹣⁵ D、2.5×10^﹣⁶

查看试题解析
3. 如图，是由5个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式计算正确的是（）

A、2a²+3a²=5a⁴ B、（﹣2ab）³=﹣6ab³ C、（3a+b）（3a﹣b）=9a²﹣b² D、a³•（﹣2a）=﹣2a³

查看试题解析
5. 如图，已知直线AB∥CD，直线m与AB、CD相交于点E、F，EG平分∠FEB，∠EFG=50°，则∠FEG的度数为（）

A、65° B、55° C、45° D、40°

查看试题解析
6. 一个不透明的袋中，装有2个黄球、3个红球和5个白球，它们除颜色外都相同．从袋中任意摸出一个球，是白球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{3}{10}$ D、 $\frac{1}{5}$

查看试题解析
7. 为了解某小区家庭使用垃圾袋的情况，小亮随机调查了该小区10户家庭一周垃圾袋的使用量，结果如下：7，9，11，8，7，14，10，8，9，7（单位：个），关于这组数据下列结论正确的是（　　）

A、极差是6 B、众数是7 C、中位数是8 D、平均数是10

查看试题解析
8. 使得关于x的一元二次方程 $\frac{1}{2}$ x²+3x+k=0无实数根的最小整数k的值为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 把抛物线y=﹣x²向左平移2个单位，再向上平移3个单位，平移后的抛物线的解析式为（）

A、y=﹣（x﹣2）²﹣3 B、y=﹣（x+2）²﹣3 C、y=﹣（x+2）²+3 D、y=﹣（x﹣2）²+3

查看试题解析
10. 如图，平行四边形ABCD的顶点A（﹣2，3），B（﹣3，1），C（0，1），规定“平行四边形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换，则连续经过2017次变换后，平行四边形ABCD的对角线的交点M的坐标为（）

A、（﹣2017，2） B、（﹣2017，﹣2） C、（﹣2018，﹣2） D、（﹣2018，2）

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 27}$ ﹣（ $\frac{1}{2}$ ）^﹣¹= ．

查看试题解析
12. 已知关于x的不等式（1﹣a）x＞3的解集为x＜ $\frac{3}{1 - a}$ ，则a的取值范围是．

查看试题解析
13. 已知二次函数y=x²+（m﹣2）x+1，当x＞1时，y随x的增大而增大，则m的取值范围是．

查看试题解析
14. 如图，矩形ABCD中，BC=4，以顶点A，B为圆心，以AD、BC长为半径作两条弧，两弧相切于点E，且E在AB上，以AB为直径作半圆恰好与DC相切，则图中阴影部分的面积为．

查看试题解析
15. 在矩形ABCD中，AB=3，BC=6，点E在边BC上，且BE=2CE，将矩形沿过点E的直线折叠，点C、D的对应点分别为C′、D′，折痕与边AD交于点F，当点B、C′、D′恰好在同一直线上时，AF的长为．

查看试题解析

三、解答题

16. 先化简（x﹣ $\frac{1}{x}$ ）÷ $\frac{x^{2} - 2 x + 1}{x^{2} - x}$ ，然后从﹣1＜x＜3的范围内选取一个合适的整数作为x的值代入并求值．

查看试题解析
17. 某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣，利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查．
造成医患关系紧张的原因（单选）
A．药价高
B．检测项目太多且收费太高
C．住院报销比例低
D．医疗费与个人收入不相称
E．其他
根据调查结果绘制出了如下两幅尚不完整的统计图．
根据以上信息解答下列问题：

(1)、这次接受调查的总人数为人；

(2)、在扇形统计图中，“A”所在扇形的圆心角的度数为；

(3)、补全条形统计图；

(4)、若该市有1000万人，请你估计选D的总人数．

查看试题解析
18. 如图，AB为⊙O的直径，E是⊙O外一点，过点E作⊙O的两条切线ED、EB，切点分别为点D，B，连接AD并延长交BE延长线于点C，连接OE．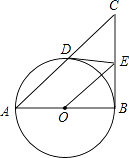

(1)、试判断OE与AC的关系，并说明理由；

(2)、填空：
①当∠BAC=时，四边形ODEB是正方形．
②当∠BAC=30°时， $\frac{A D}{D E}$ 的值为．

查看试题解析
19.
如图，在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面，小明在斜坡底A处测得该纪念碑顶部D的仰角为45°，然后他沿着坡比i=5：12的斜坡AB攀行了39米到达坡顶，在坡顶B处又测得该纪念碑顶部的仰角为68°．求坡顶B到地面AE的距离和纪念碑CD的高度．（结果精确到1米，参考数据：sin68°=0.9，cos68°=0.4，tan68°=2.5）

查看试题解析
20. “全民阅读”深入人心，读好书让人终身受益．为打造书香校园，满足同学们的读书需求，学校图书馆准备到新华书店采购文学名著和科技阅读两类图书．经了解，20本文学名著和40本科技阅读共需1520元，一本文学名著比一本科技阅读多22元（注：所采购的文学名著书价格都一样，所采购的科技阅读书价格都一样）．

(1)、求每本文学名著和科技阅读各多少元？

(2)、若学校要求购买科技阅读比文学名著多20本，科技阅读和文学名著总数不低于72本，总费用不超过2000元，请你为学校求出符合条件的购书方案．

(3)、请在（2）的条件下，请你求出此次活动学校最多需投入资金多少元？

查看试题解析
21. 平行四边形ABCD的两个顶点A、C在反比例函数y= $\frac{k}{x}$ （k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点

(1)、已知点A的坐标是（2，3），求k的值及C点的坐标；

(2)、在（1）的条件下，若△APO的面积为2，求点D到直线AC的距离．

查看试题解析
22.
已知，如图①，△ABC、△AED是两个全等的等腰直角三角形（其顶点B、E重合），∠BAC=∠AED=90°，O为BC的中点，F为AD的中点，连接OF．

(1)、
问题发现
①如图①，线段OF与EC的数量关系为；
②将△AED绕点A逆时针旋转45°，如图②，OF与EC的数量关系为；

(2)、
类比延伸
将图①中△AED绕点A逆时针旋转到如图③所示的位置，请判断线段OF与EC的数量关系，并给出证明．

(3)、拓展探究
将图①中△AED绕点A逆时针旋转，旋转角为α，0°≤α≤90°，AD= $\sqrt{2}$ ，△AED在旋转过程中，存在△ACD为直角三角形，请直接写出线段CD的长．

查看试题解析
23.
如图，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（1，0）、B（3，0）两点，与y轴交于点C（0，3）．

(1)、求抛物线的解析式；

(2)、设点P是位于直线BC下方的抛物线上一动点，过点P作y轴的平行线交直线BC于点Q，求线段PQ的最大值；

(3)、在（2）的条件下，抛物线的对称轴与直线BC交于点M，问是否存在点P，使以M、P、Q为顶点的三角形与△CBO相似？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析