2017年河南省南阳市新野县中考数学二模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1.
实数a,b,c在数轴上的对应点的位置如图所示,则a的相反数是( )
 A、a B、b C、﹣b D、c2. 若某几何体的三视图如图所示,则该几何体是( )
A、a B、b C、﹣b D、c2. 若某几何体的三视图如图所示,则该几何体是( )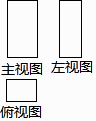 A、
A、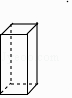 B、
B、 C、
C、 D、
D、 3. PM2.5“超细灰尘”主要来自机动车尾气尘、燃油尘、硫酸盐、餐饮油烟尘、建筑水泥尘、煤烟尘和硝酸盐等,它是雾霾有害细颗粒的重要组成部分.而PM2.5可直接被人体吸入肺部,由于其穿透力强,因此对人类的危害非常大,PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣64. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)5. 如图,这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图,如果他家去年总开支为6万元,那么用于教育的支出为( )
3. PM2.5“超细灰尘”主要来自机动车尾气尘、燃油尘、硫酸盐、餐饮油烟尘、建筑水泥尘、煤烟尘和硝酸盐等,它是雾霾有害细颗粒的重要组成部分.而PM2.5可直接被人体吸入肺部,由于其穿透力强,因此对人类的危害非常大,PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣64. 在平面直角坐标系中,若将抛物线y=2x2﹣4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(﹣2,3) B、(﹣1,4) C、(1,4) D、(4,3)5. 如图,这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图,如果他家去年总开支为6万元,那么用于教育的支出为( ) A、3万元 B、 万元 C、2.4万元 D、2万元6. 用尺规作图法作已知角∠AOB的平分线的步骤如下:
A、3万元 B、 万元 C、2.4万元 D、2万元6. 用尺规作图法作已知角∠AOB的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于 DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
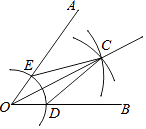 A、SAS B、ASA C、AAS D、SSS7. 如图,在▱ABCD中,AC平分∠DAB,AB=3,则▱ABCD的周长为( )
A、SAS B、ASA C、AAS D、SSS7. 如图,在▱ABCD中,AC平分∠DAB,AB=3,则▱ABCD的周长为( ) A、6 B、9 C、12 D、158. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )A、x(x﹣10)=900 B、x(x+10)=900 C、10(x+10)=900 D、2[x+(x+10)]=9009. 小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶( )A、35cm B、50cm C、25cm D、45cm10. 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y= 与线段AB有公共点,则k的取值范围是( )
A、6 B、9 C、12 D、158. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )A、x(x﹣10)=900 B、x(x+10)=900 C、10(x+10)=900 D、2[x+(x+10)]=9009. 小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶( )A、35cm B、50cm C、25cm D、45cm10. 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),双曲线y= 与线段AB有公共点,则k的取值范围是( ) A、k>0 B、k≥1 C、k≥4 D、1≤k≤4
A、k>0 B、k≥1 C、k≥4 D、1≤k≤4二、填空题
-
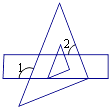
11. 计算 ﹣|﹣2|= .12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2是度.
 13. 表格记录了一名球员在罚球线上罚篮的结果.
13. 表格记录了一名球员在罚球线上罚篮的结果.投篮次数n
100
150
300
500
800
1000
投中次数m
58
96
174
302
484
601
投中频率
0.580
0.640
0.580
0.604
0.605
0.601
这名球员投篮一次,投中的概率约是 .
14. 将△ABC绕点B逆时针旋转到△A′BC′,使A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,AB=4cm,则图中阴影部分面积为 cm2 .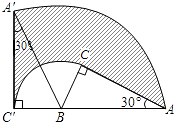 15. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
15. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .三、解答题
-
16. 先化简,再求值:(1﹣ )÷ ﹣ ,其中2x2+4x﹣1=0.17. 如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为 的中点.
 (1)、求证:AB=BC;(2)、求证:四边形BOCD是菱形.18. 某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.
(1)、求证:AB=BC;(2)、求证:四边形BOCD是菱形.18. 某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄
26
42
57
健康指数
97
79
72
表2:小王抽样调查单位10名职工的健康指数
年龄
23
25
26
32
33
37
39
42
48
52
健康指数
93
89
90
83
79
75
80
69
68
60
表3:小李抽样调查单位10名职工的健康指数
年龄
22
29
31
36
39
40
43
46
51
55
健康指数
94
90
88
85
82
78
72
76
62
60
根据上述材料回答问题:
 (1)、小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.(2)、根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.19. 关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根.(1)、求m的取值范围.(2)、如果等腰三角形ABC的两边是这个方程的两根,且腰长是7,求这个三角形的周长.20. 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
(1)、小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.(2)、根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.19. 关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根.(1)、求m的取值范围.(2)、如果等腰三角形ABC的两边是这个方程的两根,且腰长是7,求这个三角形的周长.20. 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)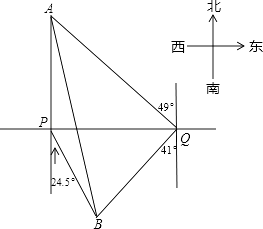 21. 小东根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)、函数y= 的自变量x的取值范围是;(2)、表格是y与x的几组对应值.
21. 小东根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)、函数y= 的自变量x的取值范围是;(2)、表格是y与x的几组对应值.x
…
﹣2
﹣1
﹣
0
1
2
3
4
…
y
…
2
4
2
m
…
表中m的值为;
(3)、如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出函数y= 的大致图象;
 (4)、结合函数图象,请写出函数y= 的一条性质: .(5)、如果方程 =a有2个解,那么a的取值范围是 .22. 解答题(1)、问题发现
(4)、结合函数图象,请写出函数y= 的一条性质: .(5)、如果方程 =a有2个解,那么a的取值范围是 .22. 解答题(1)、问题发现如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为;
②线段AC、CD、CE之间的数量关系为 .
 (2)、拓展探究
(2)、拓展探究如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
 (3)、解决问题
(3)、解决问题如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
 23. 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
23. 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处. (1)、求AD的长及抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?(3)、若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
(1)、求AD的长及抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?(3)、若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.