内蒙古自治区呼和浩特市玉泉区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-09 类型：期中考试
一、单选题
-
1. 下列标志中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
2. 在平面直角坐标系中，点P（﹣1，2）关于x轴的对称点的坐标为（ ）A、（﹣1，﹣2） B、（1，2） C、（2，﹣1） D、（﹣2，1）3. 如图，虚线部分是小刚作的辅助线，则你认为线段CD为( )
A、边AC上的高 B、边BC上的高 C、边AB上的高 D、不是△ABC的高4. 设三角形三边之长分别为3，8，1﹣2a，则a的取值范围为（ ）A、﹣6＜a＜﹣3 B、﹣5＜a＜﹣2 C、﹣2＜a＜5 D、a＜﹣5或a＞25. 用直尺和圆规作一个角的平分线如图所示，说明∠AOC＝∠BOC的依据是（ ）．
A、SSS B、ASA C、AAS D、角平分线上的点到角两边距离相等6. 如果一个等腰三角形的一个角为30°，则这个三角形的顶角为（ ）A、120° B、30° C、120°或30° D、90°7. 如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E．BC=EF；
③∠B=∠E，BC=EF，∠C=∠F；
④AB=DE，AC=DF，∠B=∠E．
其中，能使△ABC≌△DEF的条件共有（ ）
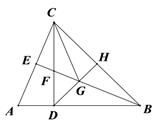
A、1组 B、2组 C、3组 D、4组8. 如图，在五边形 ABCDE 中，∠A+∠B+∠E=α，DP，CP 分别平分∠EDC，∠BCD，则∠P 的度数是（ ）
A、90°+ α B、 α﹣90° C、 α D、540° - α9. 如图，AB⊥CD，且AB=CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE=a，BF=b，EF=c，则AD的长为（ ）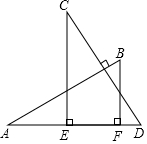
A、 B、 C、 D、10. 如图，在四边形ABCD中，∠B=∠C=90°，∠DAB与∠ADC的平分线相交于BC边上的M点，则下列结论：①∠AMD=90°；②M为BC的中点；③AB+CD=AD；④ ；⑤M到AD的距离等于BC的一半；其中正确的有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 一个多边形的内角和是外角和的3倍，则它是边形．12. 如图，△ABC≌△EDC，△ABC的周长为100cm，DE=30cm，EC=25cm，那么AC长为cm．
13. 如图，在四边形ABCD中，∠A=450 ， 直线l与边AB、AD分别相交于点M、N。则∠1 ＋∠2 =。
14. 已知点 与点 关于x轴对称,则 ．15. 如图，AM是 的中线， 的面积为4， 的面积为5，则 的面积 ．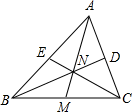
16. 如图，在Rt△ 中， ＝90°， ＝30°，在直线 或直线 上取一点 ，使得△ 是等腰三角形，则符合条件的 点有个．
三、解答题
-
17. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．
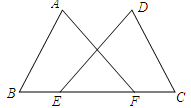18. 如图，∠A=∠B ， CE∥DA ， CE交AB于E ． 求证：△CEB是等腰三角形．
19. 如图，已知△ABC的三个顶点在格点上．
(1)、作出与△ABC关于x轴对称的图形△A1B1C1；(2)、求出A1 ， B1 ， C1三点坐标；(3)、求△ABC的面积．20. 如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF．
(1)、求证：AD平分∠BAC；(2)、直接写出AB+AC与AE之间的等量关系．
