福建省福州市平潭县2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列交通标志图案是轴对称图形的是

A、 B、 C、 D、

查看试题解析
2. 下列计算结果为 $a^{5}$ 的是（）

A、 $a^{2} \cdot a^{3}$ B、 $a^{2} + a^{3}$ C、 ${(a^{3})}^{2}$ D、 $a^{15} \div a^{3}$

查看试题解析
3. 在平面直角坐标系中，点 $M （ 1 ， 2 ）$ 关于 $x$ 轴对称点的坐标为（）

A、 $（ - 1 ， - 2 ）$ B、 $（ - 1 ， 2 ）$ C、 $（ 1 ， - 2 ）$ D、 $（ 2 ，一 1 ）$

查看试题解析
4. 如图，已知AB＝AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（）

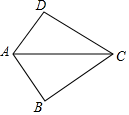A、CB＝CD B、∠BCA＝∠DCA C、∠BAC＝∠DAC D、∠B＝∠D＝90°

查看试题解析
5. 若 $(x - 1) (x + 3) = x^{2} + a x + b$ ，则a，b的值分别为（　　　　）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
6. 如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若AB＝4，CF＝3，则BD的长是（　　）

A、0.5 B、1 C、1.5 D、2

查看试题解析
7. 如图，已知射线OM，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，那么∠AOB的度数是（）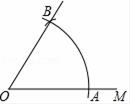

A、90° B、60° C、45° D、30°

查看试题解析
8. 已知 $x + y = - 5, x y = 3$ ，则 $x^{2} + y^{2} =$ （）

A、19 B、6 C、25 D、-19

查看试题解析
9. 如图， $A B ∥ C D$ ，BP和CP分别平分 $∠ A B C$ 和 $∠ D C B$ ，AD过点P，且与AB垂直。若点P到BC的距离是4，则AD的长为（）

A、8 B、6 C、4 D、2

查看试题解析
10. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）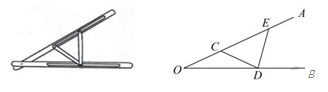

A、60° B、65° C、75° D、80°

查看试题解析

二、填空题

11. ${(- 2)}^{0}$ = ．

查看试题解析
12. 已知 $△ A B C ≌ △ D E F, ∠ A = 80^{°}$ ， $∠ E = 50^{°}$ ，则 $∠ F$ 的度数为

查看试题解析
13. 若等腰三角形的两边的边长分别为 $20 c m$ 和 $9 c m$ ，则第三边的长是 $c m$ .

查看试题解析
14. 若 $a^{2} - b^{2} = 4$ ，则 ${(a - b)}^{2} {(a + b)}^{2} =$ .

查看试题解析
15. 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF＝AC，则∠ABC＝度．

查看试题解析
16. 如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则 $△ CDM$ 周长的最小值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $(15 x^{2} y - 10 x y^{2}) \div 5 x y$

(2)、 ${(a + 2)}^{2} + a (a - 4)$

查看试题解析
18. 先化简，再求值：(2x﹣3y)²+(x+3y)(x﹣3y)，其中x=2，y=5．

查看试题解析
19. 已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．

查看试题解析
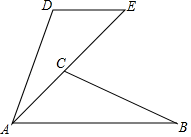20. 图1、2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．

(1)、在图1中画出以AC为腰的等腰三角形ACD，点D在小正方形的顶点上，且△ACD的面积为8．

(2)、在图2中画出以AC为腰的等腰直角三角形ABC，点B在小正方形顶点上．

查看试题解析
21. 如图，在△ABC中，AB=AC，AD是BC边上的中线，E是AC 边上的一点，且∠CBE=∠CAD．求证：BE⊥AC．

查看试题解析
22. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90^{°} ， ∠ C = 30^{°}$ .

(1)、请在图中用尺规作图的方法作出AC的垂直平分线交BC于点D，并标出D点（不写作法，保留作图痕迹）.

(2)、在（1）的条件下，连接AD，求证： $△ A B D$ 是等边三角形.

查看试题解析
23. 求证：全等三角形的对应角平分线相等。

(1)、画出适合题意的图形，并结合图形写出已知和求证。

(2)、给出证明。

查看试题解析
24. 如图，△ABC和△ADE中， $A B = A D = 6 ， B C = D E$ ， $∠ B = ∠ D = 30 °$ ，边AD与边BC交于点P（不与点B，C重合），点B，E在AD异侧，AI、CI分别平分 $∠ P A C$ ， $∠ P C A$ ．

(1)、求证： $∠ B A D = ∠ C A E$ ；

(2)、设 $A P = x$ ，请用含 $x$ 的式子表示PD，并求PD的最大值；

(3)、当 $A B ⊥ A C$ 时， $∠ A I C$ 的取值范围为 $m ° < ∠ A I C < n$ ，分别直接写出m，n的值．

查看试题解析
25. 如图，在平面直角坐标系中，点 A，B的坐标分别为（0，3），（1，0），△ABC是等腰直角三角形，∠ABC＝90°．

(1)、图1中，点C的坐标为；

(2)、如图2，点D的坐标为（0，1），点E在射线CD上，过点B 作BF⊥BE交y轴于点F．
①当点E为线段CD的中点时，求点F的坐标；

②当点E在第二象限时，请直接写出F点纵坐标y的取值范围．

查看试题解析