2017年河南省南阳市淅川县中考数学二模试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、选择题
-
1. 下列各数中，最大的数是（ ）A、|﹣3| B、﹣2 C、0 D、12. 下列运算正确的是（ ）A、a•a3=a3 B、（ab）3=a3b C、（a3）2=a6 D、a8÷a4=a23. 如图所示正三棱柱的主视图是（ ）
A、
B、
C、
D、
4. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都均为8.8环，方差分别为S甲2=0.63，S乙2=0.51，S丙2=0.48，S丁2=0.42，则四人中成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁5. 已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为（ ）A、 B、2π C、3π D、12π6. 如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为（ ）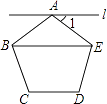
A、30° B、36° C、38° D、45°7.如图，点A是反比例函数y=的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为3，则k的值是（ ）
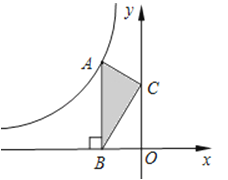A、3 B、﹣3 C、6 D、﹣68. 如图，△ABC内接于半径为5的⊙O，圆心O到弦BC的距离等于3，则∠A的正切值等于（ ）
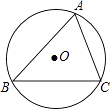A、 B、 C、 D、9. 从标有号数1到10的10张卡片中，随意抽取一张，其号数为3的倍数的概率是（ ）A、 B、 C、 D、无法确定10.如图①，四边形ABCD中，BC∥AD，∠A=90°，点P从A点出发，沿折线AB→BC→CD运动，到点D时停止，已知△PAD的面积s与点P运动的路程x的函数图象如图②所示，则点P从开始到停止运动的总路程为（ ）
A、4 B、2+ C、5 D、4+二、填空题
-
11. 计算：2﹣2﹣ = ．12. 如图，平面上直线a，b分别经过线段OK两端点（数据如图），则a，b相交所成的锐角是 ．
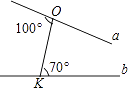13. 如图，在等腰Rt△OAA1中，∠OAA1=90°，OA=1，以OA1为直角边作等腰Rt△OA1A2 ， 以OA2为直角边作等腰Rt△OA2A3 ， …则OA6的长度为 ．
14. 二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b=0；②a+c＞b；③抛物线y=ax2+bx+c与x轴的另一个交点为（3，0）；④abc＞0．其中正确的结论是（填写序号）
15. 如图，在平行四边形ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将平行四边形ABCD沿EF折叠，得到四边形EFGC，点A的对应点为点C，点D的对应点为点G，则△CEF的面积 ．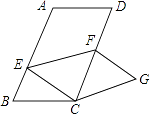
三、解答题
-
16. 先化简，再求值： ÷ ，其中m是方程x2+2x﹣3=0的根．17. 为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成了如下两幅不完整的统计图：
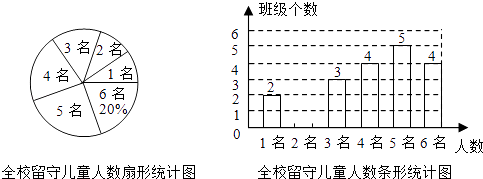(1)、将该条形统计图补充完整；(2)、求该校平均每班有多少名留守儿童？(3)、某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．18. 如图，AB是半圆O的直径，点C是半圆O上一点，∠COB=60°，点D是OC的中点，连接BD，BD的延长线交半圆O于点E，连接OE，EC，BC．
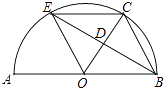(1)、求证：△BDO≌△EDC．(2)、若OB=6，则四边形OBCE的面积为 ．19. 为解决江北学校学生上学过河难的问题，乡政府决定修建一座桥，建桥过程中需测量河的宽度（即两平行河岸AB与MN之间的距离）．在测量时，选定河对岸MN上的点C处为桥的一端，在河岸点A处，测得∠CAB=30°，沿河岸AB前行30米后到达B处，在B处测得∠CBA=60°，请你根据以上测量数据求出河的宽度．（参考数据： ≈1.41， ≈1.73，结果保留整数）
20. 某小区为了绿化环境，计划分两次购进A、B两种花草，第一次分别购进A、B两种花草30棵和15棵，共花费675元；第二次分别购进A、B两种花草12棵和5棵．两次共花费940元（两次购进的A、B两种花草价格均分别相同）．(1)、A、B两种花草每棵的价格分别是多少元？(2)、若购买A、B两种花草共31棵，且B种花草的数量少于A种花草的数量的2倍，请你给出一种费用最省的方案，并求出该方案所需费用．21.如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为（4，0），顶点G的坐标为（0，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．
(1)、求图象经过点A的反比例函数的解析式；(2)、设（2）中的反比例函数图象交EF于点B，直接写出直线AB的解析式．22. 在△ABC中，∠ACB是锐角，点D在射线BC上运动，连接AD，将线段AD绕点A逆时针旋转90°，得到AE，连接EC．(1)、操作发现：
若AB=AC，∠BAC=90°，当D在线段BC上时（不与点B重合），如图①所示，请你直接写出线段CE和BD的位置关系和数量关系是 ， ；
(2)、猜想论证：
在（1）的条件下，当D在线段BC的延长线上时，如图②所示，请你判断（1）中结论是否成立，并证明你的判断．
(3)、拓展延伸：
如图③，若AB≠AC，∠BAC≠90°，点D在线段BC上运动，试探究：当锐角∠ACB等于度时，线段CE和BD之间的位置关系仍成立（点C、E重合除外）？此时若作DF⊥AD交线段CE于点F，且当AC=3 时，请直接写出线段CF的长的最大值是
23.如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），C（0，4）两点，与x轴交于另一点B，
(1)、求抛物线的解析式；(2)、求P在第一象限的抛物线上，P点的横坐标为t，过点P向x轴做垂线交直线BC于点Q，设线段PQ的长为m，求m与t之间的函数关系式并求出m的最大值；(3)、在（2）的条件下，抛物线上一点D的纵坐标为m的最大值，连接BD，在抛物线是否存在点E（不与点A，B，C重合）使得∠DBE=45°？若不存在．请说明理由；若存在请求E点的坐标．