2017年河南省安阳市林州市中考数学二模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 在实数3,﹣3,﹣ , 中最小的数是( )A、3 B、﹣3 C、 D、﹣2. 据统计,2017年河南省的夏粮收购总产量为796.24亿斤,请用科学记数法表示这个数为( )A、7.9624×1010 B、7.9624×109 C、79.624×109 D、0.79624×10113. 下列运算正确的是( )A、 B、 C、 D、4. 关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )A、m< B、m> 且m≠2 C、m≤ D、m≥ 且m≠25. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
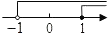 B、
B、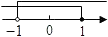 C、
C、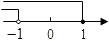 D、
D、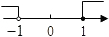 6. 下列说法不正确的是( )A、某种彩票中奖的概率是 ,买1000张该种彩票一定会中奖 B、了解一批电视机的使用寿命适合用抽样调查 C、若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定 D、在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件7. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
6. 下列说法不正确的是( )A、某种彩票中奖的概率是 ,买1000张该种彩票一定会中奖 B、了解一批电视机的使用寿命适合用抽样调查 C、若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定 D、在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件7. 如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )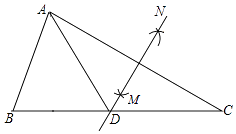 A、65° B、60° C、55° D、45°8. 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A、65° B、60° C、55° D、45°8. 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )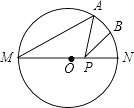 A、2 B、2 C、2 D、39. 如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,边AO在y轴上,点B1 , B2 , B3 , …都在直线y= x上,则A2017的坐标为( )
A、2 B、2 C、2 D、39. 如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,边AO在y轴上,点B1 , B2 , B3 , …都在直线y= x上,则A2017的坐标为( )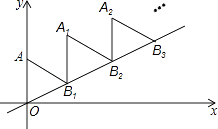 A、2015 ,2017 B、2016 ,2018 C、2017 ,2019 D、2017 ,201710. 如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )
A、2015 ,2017 B、2016 ,2018 C、2017 ,2019 D、2017 ,201710. 如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )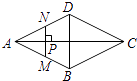 A、
A、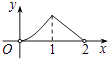 B、
B、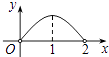 C、
C、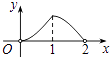 D、
D、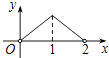
二、填空题
-
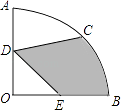
11. 函数 的自变量x的取值范围是 .12. 计算:(﹣ )﹣1﹣| |+2sin60°+(π﹣4)0= .13. 一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为 .14. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为 cm2 .
 15. 已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 .
15. 已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 .
三、解答题
-
16. 先化简,再求值: ,其中x满足x2﹣x﹣1=0.17. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
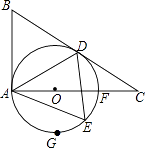 (1)、求证:BD是⊙O的切线.(2)、若AB= ,E是半圆 上一动点,连接AE,AD,DE.
(1)、求证:BD是⊙O的切线.(2)、若AB= ,E是半圆 上一动点,连接AE,AD,DE.填空:
①当 的长度是时,四边形ABDE是菱形;
②当 的长度是时,△ADE是直角三角形.
18. 当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A、基本不用;B、平均一天使用1~2小时;C、平均一天使用2~4小时;D、平均一天使用4~6小时;E、平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图(图1、2),请根据相关信息,解答下列问题: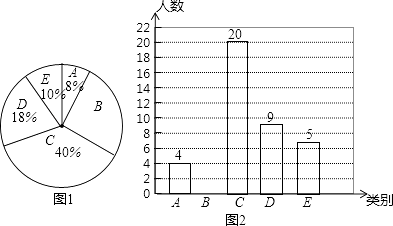 (1)、将上面的条形统计图补充完整;(2)、若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;(3)、在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.19. 如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)
(1)、将上面的条形统计图补充完整;(2)、若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;(3)、在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.19. 如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1: ,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)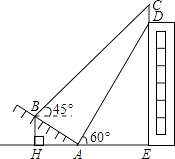 (1)、求点B距水平而AE的高度BH;(2)、求宣传牌CD的高度.
(1)、求点B距水平而AE的高度BH;(2)、求宣传牌CD的高度.(结果精确到0.1米.参考数据: ≈1.414, ≈1.732)
20. 已知:关于x的方程kx2﹣(3k﹣1)x+2(k﹣1)=0(1)、求证:无论k为任何实数,方程总有实数根;(2)、若此方程有两个实数根x1 , x2 , 且|x1﹣x2|=2,求k的值.21. 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元. (1)、求W关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;(3)、“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.22. 在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.(1)、如图1,若四边形ABCD是正方形.
(1)、求W关于x的函数关系式,并写出自变量x的取值范围;(2)、若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;(3)、“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.22. 在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.(1)、如图1,若四边形ABCD是正方形.①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.
 (2)、如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.
(2)、如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.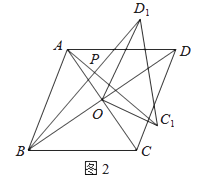 (3)、如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.
(3)、如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.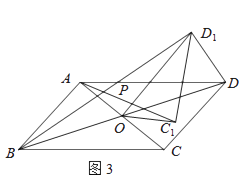 23. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.
23. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.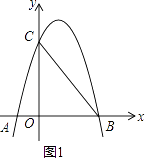 (1)、试求抛物线的解析式;(2)、点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;(3)、如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?
(1)、试求抛物线的解析式;(2)、点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;(3)、如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?