2017年山东省日照市莒县中考数学一模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 在已知实数:﹣3,0, ,﹣1中,最小的一个实数是( )A、﹣1 B、0 C、 D、﹣32. 如图,一个空心圆柱体,其主视图正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )A、1.05×105 B、0.105×10﹣4 C、1.05×10﹣5 D、105×10﹣74. 某班10名学生校服尺寸与对应人数如下表所示:
3. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )A、1.05×105 B、0.105×10﹣4 C、1.05×10﹣5 D、105×10﹣74. 某班10名学生校服尺寸与对应人数如下表所示:尺寸(cm)
160
165
170
175
180
学生人数(人)
1
3
2
2
2
则这10名学生校服尺寸的众数和中位数分别为( )
A、165,165 B、165,170 C、170,165 D、170,1705. 某果园2015年水果产量为a吨,2016年因干旱影响产量下降15%,2017年新增滴灌系统,预计产量能在2016年基础上上升20%,估计2017年该果园水果产量为( )A、(1﹣15%)(1+20%)a吨 B、(1﹣15%)20%a吨 C、(1+15%)(1﹣20%)a吨 D、(1+20%)15%a吨6. 将直线y=2x+1变成y=2x﹣1经过的变化是( )A、向上平移2个单位 B、向下平移2个单位 C、向右平移2个单位 D、向左平移2个单位7. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )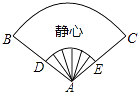 A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 已知实数a、b(a≠b)都能使方程x2﹣3x﹣1=0的左右两边相等,则 + 的值为( )A、﹣3 B、﹣1 C、1 D、39. 为了进一步落实“节能减排”工作,某单位决定对3600平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标.比较两个工程队的标书发现:乙队每天完成的工程量是甲队的2倍,这样乙队单独干比甲队单独干能提前10天完成任务.设甲队每天完成x平方米,可列方程为( )A、 ﹣ =10 B、 ﹣ =10 C、 + =10 D、10(2x+x)=360010.
A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 已知实数a、b(a≠b)都能使方程x2﹣3x﹣1=0的左右两边相等,则 + 的值为( )A、﹣3 B、﹣1 C、1 D、39. 为了进一步落实“节能减排”工作,某单位决定对3600平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标.比较两个工程队的标书发现:乙队每天完成的工程量是甲队的2倍,这样乙队单独干比甲队单独干能提前10天完成任务.设甲队每天完成x平方米,可列方程为( )A、 ﹣ =10 B、 ﹣ =10 C、 + =10 D、10(2x+x)=360010.在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的横坐标是( )
 A、2 B、2n﹣1 C、2n D、2n+111. 已知二次函数y=﹣(x﹣a)2﹣b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是( )
A、2 B、2n﹣1 C、2n D、2n+111. 已知二次函数y=﹣(x﹣a)2﹣b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是( )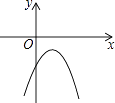 A、
A、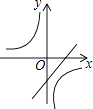 B、
B、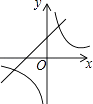 C、
C、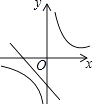 D、
D、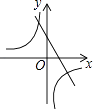 12. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2017等于( )
12. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2017等于( )
A、﹣1 B、 C、1 D、2二、填空题
-
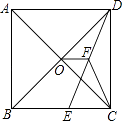
13. 分解因式:x3﹣xy2= .14. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
 15. 一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α﹣β)=sinα•cosβ﹣cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°= × + × =1.类似地,可以求得sin15°的值是 .16. 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,若OA2﹣AB2=18,则k的值为 .
15. 一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α﹣β)=sinα•cosβ﹣cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°= × + × =1.类似地,可以求得sin15°的值是 .16. 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,若OA2﹣AB2=18,则k的值为 .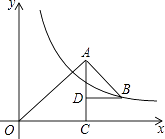
三、解答题
-
17. 根据要求进行计算:(1)、先化简再求值:a(1﹣4a)+(2a+1)(2a﹣1),其中a=3.(2)、解不等式组: .18. 从今年起,某市生物和地理会考实施改革,考试结果以等级形式呈现,分A、B、C、D四个等级.某校八年级为了迎接会考,进行了一次模拟考试,随机抽取部分学生的生物成绩进行统计,绘制成如下两幅不完整的统计图.
 (1)、这次抽样调查共抽取了名学生的生物成绩.扇形统计图中,D等级所对应的扇形圆心角度数为°;(2)、解:将条形统计图补充完整;(3)、该校八年级一班生物第一兴趣小组有甲、乙、丙、丁四人,分别是A、B、C、D四个等级,计划从四人中随机抽出两人去参加生物竞赛,请用画树状图或列表的方法,求出刚好抽到甲、乙两名学生的概率.19. 如图①,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图②.
(1)、这次抽样调查共抽取了名学生的生物成绩.扇形统计图中,D等级所对应的扇形圆心角度数为°;(2)、解:将条形统计图补充完整;(3)、该校八年级一班生物第一兴趣小组有甲、乙、丙、丁四人,分别是A、B、C、D四个等级,计划从四人中随机抽出两人去参加生物竞赛,请用画树状图或列表的方法,求出刚好抽到甲、乙两名学生的概率.19. 如图①,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图②. (1)、求证:EG=CH;(2)、已知AF=2,求AD和AB的长.20. 如图①,▱OABC的边OC在x轴的正半轴上,OC=5,反比例函数y= (x>0)的图象经过点A(1,4).
(1)、求证:EG=CH;(2)、已知AF=2,求AD和AB的长.20. 如图①,▱OABC的边OC在x轴的正半轴上,OC=5,反比例函数y= (x>0)的图象经过点A(1,4). (1)、求反比例函数的关系式和点B的坐标;(2)、如图②,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP,求△AOP的面积;21. 问题情境:如图①,P是⊙O外的一点,直线PO分别交⊙O于点A、B,可以发现PA是点P到⊙O上的点的最短距离.
(1)、求反比例函数的关系式和点B的坐标;(2)、如图②,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP,求△AOP的面积;21. 问题情境:如图①,P是⊙O外的一点,直线PO分别交⊙O于点A、B,可以发现PA是点P到⊙O上的点的最短距离.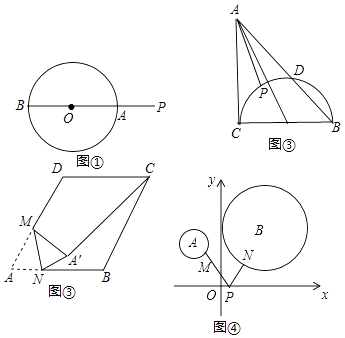 (1)、直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是 .(2)、构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)、综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于 .22. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)、直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是 .(2)、构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)、综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于 .22. 如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.