2017年山东省泰安市岱岳区中考数学二模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算 $\frac{1}{3}$ ﹣ $\frac{1}{2}$ 的结果是（）

A、6的倒数 B、6的相反数 C、﹣6的绝对值 D、﹣6的倒数

查看试题解析
2. 某种细菌直径约为0.00000067mm，若将0.000 000 67mm用科学记数法表示为6.7×10ⁿmm（n为负整数），则n的值为（）

A、﹣5 B、﹣6 C、﹣7 D、﹣8

查看试题解析
3. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、2a+3b=5ab B、 $\sqrt{12}$ ﹣ $\sqrt{3}$ = $\sqrt{3}$ C、（a+b）²=a²+b² D、a⁶÷a³=a²

查看试题解析
5. 如图，将一块含有30°角的直角三角板的两个顶点叠放在矩形的两条对边上，如果∠1=α度，∠2=β度，则（）

A、α+β=150 B、α+β=90 C、α+β=60 D、β﹣α=30

查看试题解析
6. 化简分式：（1﹣ $\frac{a^{2} + 8}{a^{2} + 4 a + 4}$ ）÷ $\frac{4 a - 4}{a^{2} + 2 a}$ 的结果为（）

A、 $\frac{a + 2}{a}$ B、 $\frac{a}{a + 2}$ C、 $\frac{a - 2}{a}$ D、 $\frac{a}{a - 2}$

查看试题解析
7. 如图是某几何体的三视图，根据图中数据，求得该几何体的体积为（）

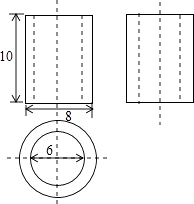A、60π B、70π C、90π D、160π

查看试题解析
8. 某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图．
依据图中信息，得出下列结论：
（1 ）接受这次调查的家长人数为200人
（2 ）在扇形统计图中，“不赞同”的家长部分所对应的扇形圆心角大小为162°
（3 ）表示“无所谓”的家长人数为40人
（4 ）随机抽查一名接受调查的家长，恰好抽到“很赞同”的家长的概率是 $\frac{1}{10}$ ．
其中正确的结论个数为（）

A、4 B、3 C、2 D、1

查看试题解析
9. 把八个完全相同的小球平分为两组，每组中每个分别写上1，2，3，4四个数字，然后分别装入不透明的口袋内搅匀，从第一个口袋内取出一个数记下数字后作为点P的横坐标x，然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标，则点P（x，y）落在直线y=﹣x+5上的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
10. 如图，在⊙O中，AC∥OB，∠BAC=25°，则∠ADB的度数为（）

A、55° B、60° C、65° D、70°

查看试题解析
11. 若不等式组 ${\begin{matrix} x + a \geq 0 \\ 1 - 2 x > x - 2 \end{matrix}$ 无解，则实数a的取值范围是（）

A、a≥﹣1 B、a＜﹣1 C、a≤1 D、a≤﹣1

查看试题解析
12. 反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示，则它们的解析式可能分别是（）

A、y= $\frac{k}{x}$ ，y=kx²﹣x B、y= $\frac{k}{x}$ ，y=kx²+x C、y=﹣ $\frac{k}{x}$ ，y=kx²+x D、y=﹣ $\frac{k}{x}$ ，y=﹣kx²﹣x

查看试题解析
13.
一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（）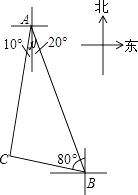

A、10 $\sqrt{3}$ 海里/小时 B、30海里/小时 C、20 $\sqrt{3}$ 海里/小时 D、30 $\sqrt{3}$ 海里/小时

查看试题解析
14. 若a，b（a＜b）是关于x的一元二次方程（x﹣m）（x﹣n）+1=0的两个根，且m＜n，则m，n，b，a的大小关系是（）

A、a＜b＜m＜n B、b＜a＜n＜m C、a＜m＜n＜b D、m＜a＜b＜n

查看试题解析
15. 如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF．如图2，展开后再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为点M，EM交AB于N，则tan∠ANE=（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{5}{6}$

查看试题解析
16. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E．若CE=4，DE=2，则AD的长是（）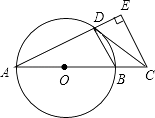

A、2 $\sqrt{2}$ B、6 C、3 D、6 $\sqrt{2}$

查看试题解析
17.
如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=3，AD=4，BC=3 $\sqrt{3}$ ，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
18. 在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AB，交AC于E．若AB=2 $\sqrt{6}$ ，AC=2 $\sqrt{5}$ ，线段DE的长为（）

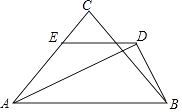A、2.5 B、2.4 C、 $\sqrt{6}$ D、 $\sqrt{5}$

查看试题解析
19. 如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，x=﹣1是对称轴，下列结论：① $\frac{a}{c}$ ＜0；②a﹣b+c=﹣9a；③若（﹣3，y₁），（ $\frac{3}{2}$ ，y₂）是抛物线上两点，则y₁＞y₂；④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a（x²﹣9）．其中正确的是（）

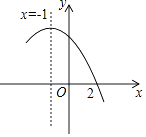A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析
20. 如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD= $\sqrt{2}$ AE²；④∠DFE=2∠DAC；⑤若连接CH，则CH∥EF，其中正确的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

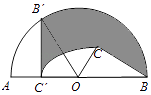
21. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} m x + n y = 7 \\ n x - m y = 1 \end{matrix}$ 的解，则m+3n的立方根为．

查看试题解析
22. 如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm² ．

查看试题解析
23. 我区大力推进义务教育均衡发展，加强学习标准化建设，计划用三年时间对全区学校的设施和设备进行全面改造.2015年区政府已投资5亿元人民币，若每年投资的增长率相同，2017年政府投资7.2亿元人民币，那么预计2018年应投资亿元．

查看试题解析
24.
如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系式是．

查看试题解析

三、解答题

25. 随着“一带一路”的进一步推进，我国瓷器（“china”）更为“一带一路”沿线人民所推崇，一外国商户看准这一商机，向我国一瓷器经销商咨询工艺品茶具，得到如下信息：
①每个茶壶的批发价比茶杯多110元；
②一套茶具包括一个茶壶与四个茶杯；
③600元批发茶壶的数量与160元批发茶杯的数量相同．
根据以上信息：

(1)、求茶壶与茶杯的批发价；

(2)、若该商户购进茶杯的数量是茶壶数量的5倍还多20个，并且总数不超过200个，该商户打算将一半的茶具按每套500元成套销售，其余按每个茶壶270元，每个茶杯70元零售，请帮助他设计一种获取利润最大的方案，并求出最大利润．

查看试题解析
26. 如图，反比例函数y= $\frac{k}{x}$ 的图象与过两点A（0，﹣2），B（﹣1，0）的一次函数的图象在第二象限内相交于点M（m，4）．

(1)、求反比例函数与一次函数的表达式；

(2)、在双曲线（x＜0）上是否存在点N，使MN⊥MB，若存在，请求出N点坐标，若不存在，说明理由．

查看试题解析
27. 在菱形ABCD中，P是直线BD上一点，点E在射线AD上，连接PC．

(1)、如图1，当∠BAD=90°时，连接PE，交CD与点F，若∠CPE=90°，求证：PC=PE；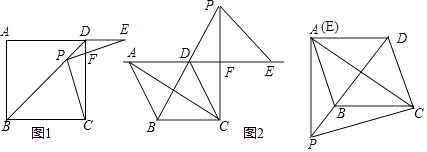

(2)、如图2，当∠BAD=60°时，连接PE，交CD与点F，若∠CPE=60°，设AC=CE=4，求BP的长．

查看试题解析
28. 如图，C为线段BD上一动点，过B、D分别作BD的垂线，使AB=BC，DE=DB，连接AD、AC、BE，过B作AD的垂线，垂足为F，连接CE、EF．

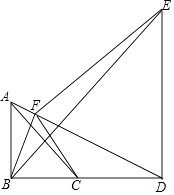(1)、求证：AC•DF= $\sqrt{2}$ BF•BD；

(2)、点C运动的过程中，∠CFE的度数保持不变，求出这个度数；

(3)、当点C运动到什么位置时，CE∥BF？并说明理由．

查看试题解析
29.
如图，平面直角坐标系中，二次函数y=﹣ $\frac{1}{4}$ x²+bx+c的图线与坐标轴分别交于点A、B、C，其中点A（0，8），OB= $\frac{1}{2}$ OA．

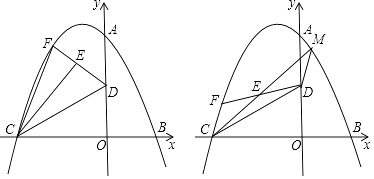(1)、求二次函数的表达式；

(2)、若OD=OB，点F为该二次函数在第二象限内图象上的动点，E为DF的中点，当△CEF的面积最大时，求出点E的坐标；

(3)、将三角形CEF绕E旋转180°，C点落在M处，若M恰好在该抛物线上，求出此时△CEF的面积．

查看试题解析