2017年山东省泰安市东平县中考数学二模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. (﹣ )﹣1的倒数是( )A、 B、 C、﹣ D、﹣2. 下列计算正确的是( )A、(﹣3a)2+4a2=a2 B、3a2﹣(﹣2a)2=﹣a2 C、3a•4a2=12a2 D、(3a2)2÷4a2= a23. 已知点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列图形是几家电信公司的标志,其中既是轴对称图形又是中心对称图形的是( )A、
4. 下列图形是几家电信公司的标志,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 化简 ÷(1+ )的结果是( )A、 B、 C、 D、6. 长方体的主视图、俯视图如图所示(单位:m),则其左视图面积是( )
5. 化简 ÷(1+ )的结果是( )A、 B、 C、 D、6. 长方体的主视图、俯视图如图所示(单位:m),则其左视图面积是( ) A、4m2 B、12m2 C、1m2 D、3m27. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1968. 2017年“端午节”期间,小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家都抽到东营港的概率是( )A、 B、 C、 D、9. 已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )A、0.000124 B、0.0124 C、﹣0.00124 D、0.0012410. 某班七个合作学习小组人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )A、5 B、5.5 C、6 D、711. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
A、4m2 B、12m2 C、1m2 D、3m27. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x2)=196 B、50+50(1+x2)=196 C、50+50(1+x)+50(1+x)2=196 D、50+50(1+x)+50(1+2x)=1968. 2017年“端午节”期间,小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家都抽到东营港的概率是( )A、 B、 C、 D、9. 已知空气的单位体积质量为1.24×10﹣3克/厘米3 , 1.24×10﹣3用小数表示为( )A、0.000124 B、0.0124 C、﹣0.00124 D、0.0012410. 某班七个合作学习小组人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )A、5 B、5.5 C、6 D、711. 把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( ) A、 B、5 C、4 D、12.
A、 B、5 C、4 D、12.如图,直线y= 与双曲线y= (k>0,x>0)交于点A,将直线y= 向上平移4个单位长度后,与y轴交于点C,与双曲线y= (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
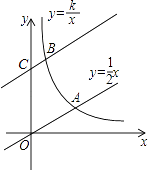 A、3 B、6 C、 D、13. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A、3 B、6 C、 D、13. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( ) A、 cm B、 cm C、 cm D、4cm14. 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A、 cm B、 cm C、 cm D、4cm14. 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( ) A、OM的长 B、2OM的长 C、CD的长 D、2CD的长15. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、
A、OM的长 B、2OM的长 C、CD的长 D、2CD的长15. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、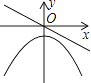 B、
B、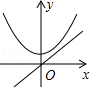 C、
C、 D、
D、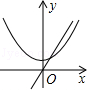 16. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
16. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD;
其中正确结论的是( )
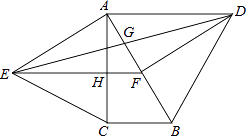 A、①②③ B、①②④ C、①③④ D、②③④17. 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10 cm,且tan∠EFC= ,那么该矩形的周长为( )
A、①②③ B、①②④ C、①③④ D、②③④17. 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10 cm,且tan∠EFC= ,那么该矩形的周长为( ) A、72cm B、36cm C、20cm D、16cm18. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE , 其中正确结论有( )
A、72cm B、36cm C、20cm D、16cm18. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE , 其中正确结论有( )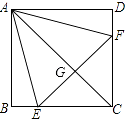 A、2个 B、3个 C、4个 D、5个19.
A、2个 B、3个 C、4个 D、5个19.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣ ,y2)、点C( ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
 A、2个 B、3个 C、4个 D、5个20.
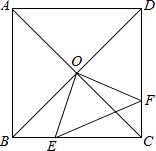
A、2个 B、3个 C、4个 D、5个20.如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
 A、
A、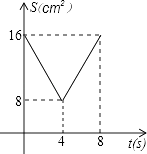 B、
B、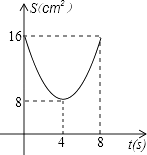 C、
C、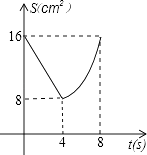 D、
D、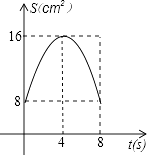
二、填空题
-
21. 因式分解2x4﹣2= .22. 方程 = 的解为 .23. 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r= 时,S为 .
 24.
24.如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1 , 以A1B、BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2 , 以A2B1、B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则C2017的坐标是 .

三、解答题
-
25. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)、甲、乙两队单独完成此项任务需要多少天?(2)、若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?26. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
 (1)、求反比例函数y= 的解析式;(2)、求cos∠OAB的值;(3)、求经过C、D两点的一次函数解析式.27.
(1)、求反比例函数y= 的解析式;(2)、求cos∠OAB的值;(3)、求经过C、D两点的一次函数解析式.27.已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1),易证BD+AB= CB,过程如下:
过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,
∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,
∴BD+AB= CB.
∴∠EAC=∠BDC
又∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE= CB.
又∵BE=AE+AB,
∴BE=BD+AB.
 (1)、当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.(2)、MN在绕点A旋转过程中,当∠BCD=30°,BD= 时,则CD= , CB= .28. 如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)、当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.(2)、MN在绕点A旋转过程中,当∠BCD=30°,BD= 时,则CD= , CB= .28. 如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E. (1)、求证:△ABF∽△COE;(2)、当O为AC的中点, 时,如图2,求 的值;(3)、当O为AC边中点, 时,请直接写出 的值.29.
(1)、求证:△ABF∽△COE;(2)、当O为AC的中点, 时,如图2,求 的值;(3)、当O为AC边中点, 时,请直接写出 的值.29.如图,已知抛物线y= x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
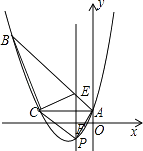 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.