2017年新疆乌鲁木齐市天山区中考数学一模试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、选择题
-
1. 在﹣3，2，﹣1，3这四个数中，比﹣2小的数是（ ）A、﹣3 B、2 C、﹣1 D、32. 如图所示的几何体是由一些正方体组合而成的立体图形，则这个几何体的俯视图是（ ）
A、
B、
C、
D、
3. 若分式 在实数范围内有意义，则x的取值范围为（ ）A、x＞2 B、x＞﹣2 C、x≠2 D、x≠﹣24. 下列说法中，正确的是（ ）A、一个游戏中奖的概率是 ，则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径，应采用全面调查的方式 C、一组数据8，7，7，10，6，7，9的众数和中位数都是7 D、若甲组数据的方差是0.1，乙组数据的方差是0.2，则乙组数据比甲组数据波动小5. 下列计算正确的是（ ）A、x3•x5=x15 B、（x3）5=x8 C、x3+x5=x8 D、x5÷x3=x26. 如图，∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于（ ）
A、5 B、4 C、3 D、27.如图，在平面直角坐标系中，▱OABC的顶点A在x轴上，顶点B的坐标为（6，4）．若直线l经过点（1，0），且将▱OABC分割成面积相等的两部分，则直线l的函数解析式是（ ）
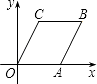A、y=x+1 B、 C、y=3x﹣3 D、y=x﹣18. 已知2是关于x的方程x2﹣2mx+3m=0的一个根，并且这个方程的两个根恰好是等腰三角形ABC的两条边长，则三角形ABC的周长为（ ）A、10 B、14 C、10或14 D、8或109. 如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于 AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）
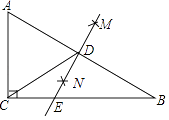A、AD=BD B、BD=CD C、∠A=∠BED D、∠ECD=∠EDC10. 已知二次函数y=ax2+bx+c（a≠0）与x轴一个交点在﹣1，﹣2之间，对称轴为直线x=1，图象如图，给出以下结论：①b2﹣4ac＞0；②abc＞0；③2a﹣b=0；④9a+3b+c＜0．其中结论正确的个数有（ ）
A、1 B、2 C、3 D、4二、填空题
-
11. 因式分解：x2y﹣4y= ．12. 有5张看上去无差别的卡片，上面分别写着0，π， ， ，1.333．随机抽取1张，则取出的数是无理数的概率是 ．13. 如图，AB是⊙O的直径，AB=15，AC=9，则cos∠ADC= ．
14. 如图，在平面直角坐标系中，点P在函数y= （x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结PC并延长交x轴于点D，则△APD的面积为 ．
15. 如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF= ．
三、解答题
-
16. 计算：4sin60°+|3﹣ |﹣（ ）﹣1+（π﹣2017）0 ．17. 已知x2﹣4x﹣1=0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．18. 如图，已知E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．
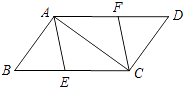(1)、求证：四边形AECF是平行四边形；(2)、若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长．19. 在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m2 ．
(1)、求这地面矩形的长；(2)、有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？20. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：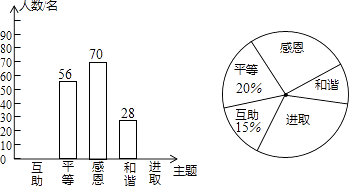
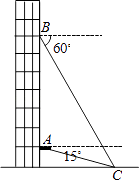
(1)、这次调查的学生共有多少名？(2)、请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．(3)、如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．21.从一幢建筑大楼的两个观察点A，B观察地面的花坛（点C），测得俯角分别为15°和60°，如图，直线AB与地面垂直，AB=50米，试求出点B到点C的距离．（结果保留根号）
22.一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．
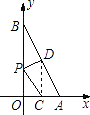(1)、求该函数的解析式；(2)、O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点的坐标．23. 如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF．
(1)、求证：CB是⊙O的切线；(2)、若∠ECB=60°，AB=6，求图中阴影部分的面积．24.如图，抛物线y=ax2+bx+3交x轴于A（﹣1，0）和B（5，0），交y轴于点C，点D是线段OB上一动点，连接CD，将CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴，垂足为H，过点C作CF⊥l于F，连接DF，CE交于点G．
(1)、求抛物线解析式；(2)、求线段DF的长；(3)、当DG= 时，①求tan∠CGD的值；
②试探究在x轴上方的抛物线上，是否存在点P，使∠EDP=45°？若存在，请写出点P的坐标；若不存在，请说明理由．