2017年湖北省黄石市九年级五月调研数学试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 2017的相反数是( )A、 B、﹣ C、﹣2017 D、20172. 下列学生剪纸作品中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、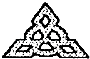 D、
D、 3. 为推进黄石经济社会转型,2016年9月26日我市举办了主题为“转型黄石•灵秀湖 北”的园博会.据 悉,举办该会总共投资了7.65亿元.其中7.65亿元用科学记数法表示是( )A、7.65×108 B、76.5×107 C、0.765×109 D、765×1064. 下列运算正确的是( )A、a6÷a2=a3 B、5a2﹣3a2=2a C、(﹣a)2•a3=a5 D、5a+2b=7ab5. 如图,由几个相同的小正方体搭成的一个几何体,它的左视图为( )
3. 为推进黄石经济社会转型,2016年9月26日我市举办了主题为“转型黄石•灵秀湖 北”的园博会.据 悉,举办该会总共投资了7.65亿元.其中7.65亿元用科学记数法表示是( )A、7.65×108 B、76.5×107 C、0.765×109 D、765×1064. 下列运算正确的是( )A、a6÷a2=a3 B、5a2﹣3a2=2a C、(﹣a)2•a3=a5 D、5a+2b=7ab5. 如图,由几个相同的小正方体搭成的一个几何体,它的左视图为( )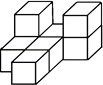 A、
A、 B、
B、 C、
C、 D、
D、 6. 某鞋店试销一种新款女鞋,销售情况如图所示,鞋店经理最关心的是哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
6. 某鞋店试销一种新款女鞋,销售情况如图所示,鞋店经理最关心的是哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )型号
34
35
36
37
38
39
40
41
数量(双)
3
5
10
15
8
3
2
1
A、平均数 B、众数 C、中位数 D、方差7. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )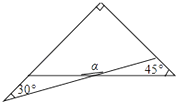 A、165° B、120° C、150° D、135°8. 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A、165° B、120° C、150° D、135°8. 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( ) A、 B、 C、 D、9. 小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
A、 B、 C、 D、9. 小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤ .
你认为其中正确信息的个数有( )
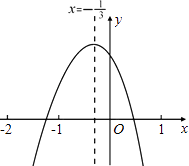 A、2个 B、3个 C、4个 D、5个10.
A、2个 B、3个 C、4个 D、5个10.如图,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0<x≤10,阴影部分的面积为y,则能反映y与x之间函数关系的大致图象是( )
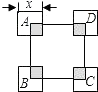 A、
A、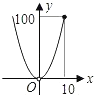 B、
B、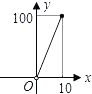 C、
C、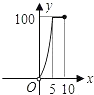 D、
D、
二、填空题:
-
11. 分解因式2x2﹣ = .12. 分式方程 的解是 .13. 已知m、n是关于x的一元二次方程x2﹣3x+a=0的两个解,若(m﹣1)(n﹣1)=﹣6,则a的值为 .14. 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是米(结果保留根号).
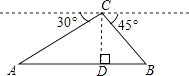 15. 一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“石”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.甲从中任取一球,不放回,再从中任取一球,则甲取出的两个球上的汉字恰能组成“灵秀”或“黄石”的概率为 .16. 如图所示,已知:点A(0,0),B( ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
15. 一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“石”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.甲从中任取一球,不放回,再从中任取一球,则甲取出的两个球上的汉字恰能组成“灵秀”或“黄石”的概率为 .16. 如图所示,已知:点A(0,0),B( ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …,则第n个等边三角形的边长等于 .
三、解答题
-
17. 计算:| ﹣5|+2cos30°+( )﹣1+(9﹣ )0+ .18. 先化简,后求值: ,其中a=3.19. 解不等式组,并在数轴上画出它的解集: .20. 已知﹣3x2+mx﹣6=0的一个根是1,求m及另一个根.21. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
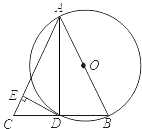 (1)、求证:AB=AC;(2)、求证:DE为⊙O的切线;(3)、若⊙O的半径为5,∠BAC=60°,求DE的长.22. “校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
(1)、求证:AB=AC;(2)、求证:DE为⊙O的切线;(3)、若⊙O的半径为5,∠BAC=60°,求DE的长.22. “校园手机”现象越来越受到社会的关注.“寒假”期间,某校小记者随机调查了某地区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图: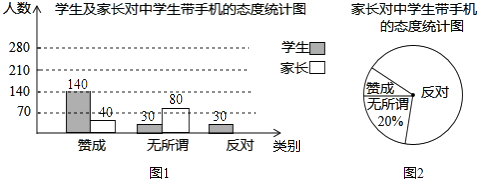 (1)、求这次调查的家长人数,并补全图1;(2)、求图2中表示家长“赞成”的圆心角的度数;(3)、已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?23. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(1)、求这次调查的家长人数,并补全图1;(2)、求图2中表示家长“赞成”的圆心角的度数;(3)、已知某地区共6500名家长,估计其中反对中学生带手机的大约有多少名家长?23. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x
销售量y(件)
销售玩具获得利润w(元)
(2)、在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.(3)、在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?24. 如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. (1)、求证:AC=AD+CE;(2)、若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(1)、求证:AC=AD+CE;(2)、若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;(i)当点P与A、B两点不重合时,求 的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
25. 如图,已知直线l:y=kx+b(k<0,b>0,且k、b为常数)与y轴、x轴分别交于A点、B点,双曲线C:y= (x>0).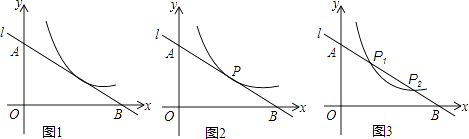 (1)、当k=﹣1,b=2 时,求直线l与双曲线C公共点的坐标;(2)、当b=2 时,求证:不论k为任何小于零的实数,直线l与双曲线C只有一个公共点(设为P),并求公共点P的坐标(用k的式子表示).(3)、①在(2)的条件下,试猜想线段PA、PB是否相等.若相等,请加以证明;若不相等,请说明理由;
(1)、当k=﹣1,b=2 时,求直线l与双曲线C公共点的坐标;(2)、当b=2 时,求证:不论k为任何小于零的实数,直线l与双曲线C只有一个公共点(设为P),并求公共点P的坐标(用k的式子表示).(3)、①在(2)的条件下,试猜想线段PA、PB是否相等.若相等,请加以证明;若不相等,请说明理由;②若直线l与双曲线C相交于两点P1、P2 , 猜想并证明P1A与P2B之间的数量关系.