2017年黑龙江省哈尔滨市呼兰区中考数学模拟试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 向东走5m记作+5m,那么向西走3m记作( )A、+3m B、﹣3m C、﹣(﹣3)m D、|﹣3|m2. 下列运算正确的是( )A、2x2•x3=2x5 B、(x﹣2)2=x2﹣4 C、x2+x3=x5 D、(x3)4=x73.
下列图形中,既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个4. 由四个相同的小正方体堆成的物体如图所示,它的俯视图是( )
A、1个 B、2个 C、3个 D、4个4. 由四个相同的小正方体堆成的物体如图所示,它的俯视图是( )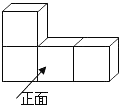 A、
A、 B、
B、 C、
C、 D、
D、 5. 某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )A、85%a10%×90 B、90×85%×10%=a C、85%(90﹣a)=10% D、(1+10%)a=90×85%6. 不等式组 的解集在数轴上表示正确的是( )A、
5. 某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )A、85%a10%×90 B、90×85%×10%=a C、85%(90﹣a)=10% D、(1+10%)a=90×85%6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、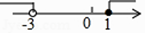 7. 如图,点A是反比例函数 (x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( )
7. 如图,点A是反比例函数 (x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为( ) A、1 B、2 C、4 D、不能确定8. 如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A、1 B、2 C、4 D、不能确定8. 如图,滑雪场有一坡角为20°的滑雪道,滑雪道的长AC为100米,则滑雪道的坡顶到坡底的竖直高度AB的长为( ) A、 B、 C、1OOcos20° D、100sin20°9. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( )
A、 B、 C、1OOcos20° D、100sin20°9. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( ) A、 B、 C、 D、10. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是( )
A、 B、 C、 D、10. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是( ) A、甲队率先到达终点 B、甲队比乙队多走了200米路程 C、乙队比甲队少用0.2分钟 D、比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快
A、甲队率先到达终点 B、甲队比乙队多走了200米路程 C、乙队比甲队少用0.2分钟 D、比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快二、填空题
-
11. 将886 000 000用科学记数法表示为 .12. 在函数y= 中,自变量x的取值范围是 .13. 化简计算:2 +4 = .14. 分解因式:ax2﹣2a2x+a3= .15. 已知扇形的面积为12πcm2 , 半径为12cm,则该扇形的圆心角是 .16. 抛物线y=x2﹣2x﹣1的对称轴为 .17. 甲、乙、丙、丁4名同学进行一次乒乓球单打比赛,要从中随机选出2名同学打第一场比赛,其中有乙同学参加的概率是 .18. 矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP= .19. 如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF= .
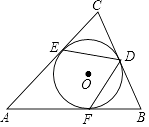 20. 已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5 ,tan∠DCB= ,则CE= .
20. 已知:如图,在△ABC中,∠BAC=90°,点D在AB上,点E在CA的延长线上,连接DC、DE,∠EDC=45°,BD=EC,DE=5 ,tan∠DCB= ,则CE= .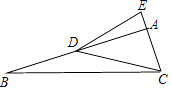
三、解答题
-
21. 先化简,再求值:(2﹣ )÷ ,其中x=2sin30°+tan60°.22. 如图,每个小方格都是边长为1的小正方形.
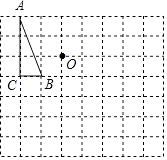 (1)、△ABC向右平移6个单位,画出平移后的△A1B1C1;(2)、将△A1B1C1绕点O顺时针旋转90°,画出旋转后的△A2B2C2;(3)、连接A1B、A2B、A1A2 , 并直接写出△BA1A2的面积.23. 为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
(1)、△ABC向右平移6个单位,画出平移后的△A1B1C1;(2)、将△A1B1C1绕点O顺时针旋转90°,画出旋转后的△A2B2C2;(3)、连接A1B、A2B、A1A2 , 并直接写出△BA1A2的面积.23. 为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:克服酒驾﹣﹣你认为哪种方式最好?(单选)
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”.
C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾.
E查出酒驾追究一同就餐人的连带责任.
随机抽取部分问卷,整理并制作了如下统计图:
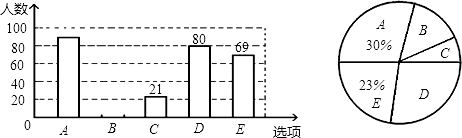
根据上述信息,解答下列问题:
(1)、本次调查的样本容量是多少?(2)、补全条形图,并计算B选项所对应扇形圆心角的度数;(3)、若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?24. 已知:如图,在▱ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.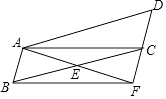 (1)、求证:四边形ABFC是平行四边形;(2)、在不添加任何辅助线的情况下,请直接写出图中与△ABC面积相等的三角形.25. 某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.(1)、今年5月份A款汽车每辆售价多少万元?(2)、为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?26. 如图1,四边形ABCD为⊙O内接四边形,连接AC、CO、BO,点C为弧BD的中点.
(1)、求证:四边形ABFC是平行四边形;(2)、在不添加任何辅助线的情况下,请直接写出图中与△ABC面积相等的三角形.25. 某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.(1)、今年5月份A款汽车每辆售价多少万元?(2)、为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?26. 如图1,四边形ABCD为⊙O内接四边形,连接AC、CO、BO,点C为弧BD的中点. (1)、求证:∠DAC=∠ACO+∠ABO;(2)、如图2,点E在OC上,连接EB,延长CO交AB于点F,若∠DAB=∠OBA+∠EBA.求证:EF=EB;
(1)、求证:∠DAC=∠ACO+∠ABO;(2)、如图2,点E在OC上,连接EB,延长CO交AB于点F,若∠DAB=∠OBA+∠EBA.求证:EF=EB;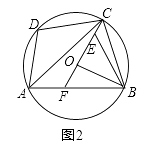 (3)、在(2)的条件下,如图3,若OE+EB=AB,CE=2,AB=13,求AD的长.
(3)、在(2)的条件下,如图3,若OE+EB=AB,CE=2,AB=13,求AD的长.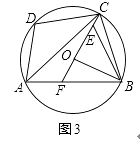 27. 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点,与y轴交于点C,BO=CO.
27. 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点,与y轴交于点C,BO=CO. (1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.
(1)、求抛物线的解析式;(2)、点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.