2017年浙江省金华市义乌市中考数学模拟试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数为( )A、﹣2 B、2 C、 D、﹣12. 2016年,义乌市经济总体平稳,全年实现地区生产总值1118亿元.将1118亿元用科学记数法表示应为(单位:元)( )A、1.118×103 B、1.118×1010 C、1.118×1011 D、1.118×10123. 下面四个几何体中,主视图与其它几何体的主视图不同的是( )A、
 B、
B、 C、
C、 D、
D、 4. 一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是( )A、 B、 C、 D、5. 将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )A、y=x2﹣1 B、y=x2+1 C、y=(x﹣1)2 D、y=(x+1)26. 一组数据2,6,2,5,4,则这组数据的中位数是( )A、2 B、4 C、5 D、67. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
4. 一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是( )A、 B、 C、 D、5. 将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )A、y=x2﹣1 B、y=x2+1 C、y=(x﹣1)2 D、y=(x+1)26. 一组数据2,6,2,5,4,则这组数据的中位数是( )A、2 B、4 C、5 D、67. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )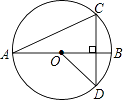 A、160° B、150° C、140° D、120°8. 如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于P.则与三角形PBC的面积相等的长方形是( )
A、160° B、150° C、140° D、120°8. 如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于P.则与三角形PBC的面积相等的长方形是( ) A、
A、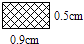 B、
B、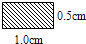 C、
C、 D、
D、 9. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( )
9. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( ) A、 B、 C、 D、10. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C是y轴上一点.将坐标平面沿直线AC折叠,使点B刚好落在x负半轴上,则点C的坐标为( )A、(0, ) B、(0, ) C、(0, ) D、(0, )
A、 B、 C、 D、10. 在平面直角坐标系中,已知直线y=﹣ x+3与x轴、y轴分别交于A、B两点,点C是y轴上一点.将坐标平面沿直线AC折叠,使点B刚好落在x负半轴上,则点C的坐标为( )A、(0, ) B、(0, ) C、(0, ) D、(0, )二、填空题
-
11. 不等式1﹣2x≥3的解是 .12. 如图,▱ABCD的对角线BD上有两点E、F,请你添加一个条件,使四边形AECF是平行四边形,你添加的条件是 .
 13. 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为 .
13. 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为 .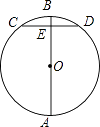 14. 在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果当 x≥0时,y′=y;当 x<0时,y′=﹣y,那么称点Q为点P的“关联点”.
14. 在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果当 x≥0时,y′=y;当 x<0时,y′=﹣y,那么称点Q为点P的“关联点”.例如:点(﹣5,6)的“关联点”为(﹣5,﹣6).如果点N(n+1,2)是一次函数y=x+3图象上点M的“关联点”,则点M的坐标为 .
15. 如图,在菱形ABCD中,∠DAB=120°,点E平分DC,点P在BD上,且PE+PC=1,那么边长AB的最大值是 .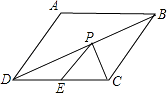 16. 如图点A(1,2)、B(2,1)在反比例函数y= 图象上,点P是反比例函数y= 在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
16. 如图点A(1,2)、B(2,1)在反比例函数y= 图象上,点P是反比例函数y= 在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.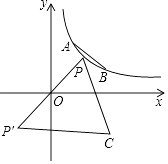
(1)、当点P与点A重合时,点C的坐标是 .(2)、已知点G是线段AB上的动点,点F在y轴上,若以A、G、F、C这样的四个点为顶点的四边形是平行四边形,则点C的纵坐标y的取值范围是 .
三、解答题
-
17. 根据要求进行计算:(1)、计算:(﹣2)2+2tan45°+(π﹣3.14)0;(2)、解方程: + =2.18. 为了解学生参加户外活动的情况,某市教育行政部门对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成下列两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
 (1)、这次抽样共调查了多少名学生,并补全条形统计图;(2)、计算扇形
(1)、这次抽样共调查了多少名学生,并补全条形统计图;(2)、计算扇形统计图中表示户外活动时间0.5小时的扇形圆心角度数;
(3)、求出本次调查学生参加户外活动的平均时间.19. 如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).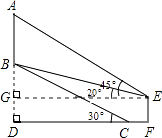 (1)、求树AB与测角仪EF的水平距离DF的长;(2)、求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36, ≈1.73)20. 甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
(1)、求树AB与测角仪EF的水平距离DF的长;(2)、求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36, ≈1.73)20. 甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.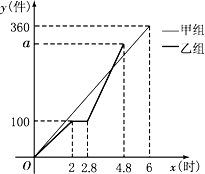 (1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;(3)、甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?21. 某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
(1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;(3)、甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?21. 某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:价格x(元/个)
…
30
40
50
60
…
销售量y(万个)
…
5
4
3
2
…
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)、观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.(2)、求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(3)、该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?22. 已知△ABC中,AB=AC,BC=6.点P从点B出发沿射线BA移动,同时点Q从点C出发沿线段AC的延长线移动,点P、Q移动的速度相同,PQ与直线BC相交于点D.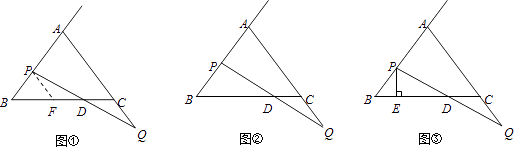 (1)、如图①,过点P作PF∥AQ交BC于点F,求证:△PDF≌△QDC;(2)、如图②,当点P为AB的中点时,求CD的长;(3)、如图③,过点P作PE⊥BC于点E,在点P从点B向点A移动的过程中,线段DE的长度是否保持不变?若保持不变,请求出DE的长度,若改变,请说明理由.23. 已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B.点A、B关于原点O的对称点分别是点C,D.若点A,B,C,D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)、如图①,过点P作PF∥AQ交BC于点F,求证:△PDF≌△QDC;(2)、如图②,当点P为AB的中点时,求CD的长;(3)、如图③,过点P作PE⊥BC于点E,在点P从点B向点A移动的过程中,线段DE的长度是否保持不变?若保持不变,请求出DE的长度,若改变,请说明理由.23. 已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B.点A、B关于原点O的对称点分别是点C,D.若点A,B,C,D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.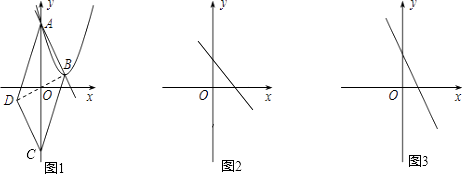 (1)、如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式;(2)、如图2,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣x+5,伴随四边形的面积为20,求此抛物线的解析式;(3)、如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.用含b的代数式表示m,n的值.24. 如图,在平面直角坐标系中,矩形OABC的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t).
(1)、如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式;(2)、如图2,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣x+5,伴随四边形的面积为20,求此抛物线的解析式;(3)、如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.用含b的代数式表示m,n的值.24. 如图,在平面直角坐标系中,矩形OABC的四个顶点坐标分别为O(0,0),A(4,0),B(4,3),C(0,3),G是对角线AC的中点,动直线MN平行于AC且交矩形OABC的一组邻边于E、F,交y轴、x轴于M、N.设点M的坐标为(0,t).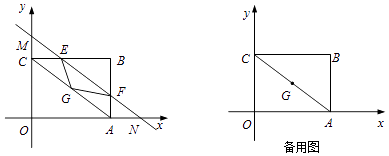 (1)、当t=2时求△EFG的面积S;(2)、当△EFG为直角三角形时,求t的值;(3)、当点G关于直线EF的对称点G′恰好落在矩形OABC的一条边所在直线上时,直接y写出t的值.
(1)、当t=2时求△EFG的面积S;(2)、当△EFG为直角三角形时,求t的值;(3)、当点G关于直线EF的对称点G′恰好落在矩形OABC的一条边所在直线上时,直接y写出t的值.