2016-2017学年广西桂林市灌阳县八年级下学期期中数学试卷
试卷更新日期：2017-07-24 类型：期中考试
一、选择题
-
1. 下列图案中，不是中心对称图形的是（ ）A、
B、
C、
D、
2. 一个多边形的内角和是外角和的2倍，这个多边形是（ ）A、三角形 B、四边形 C、五边形 D、六边形3. 在Rt△ABC中，∠C=90°，AC=3，BC=4，CD是中线，则CD的长为（ ）A、2.5 B、3 C、4 D、54. 正方形是轴对称图形，它的对称轴共有（ ）A、1条 B、2条 C、3条 D、4条5. 将一个直角三角板和一把直尺如图放置，如果∠α=47°，则∠β的度数是（ ）
A、43° B、47° C、30° D、60°6. 下列说法正确的是（ ）A、对角线相等的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、对角线互相垂直的四边形是平行四边形 D、对角线互相垂直且相等的四边形是平行四边形7. 若顺次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定是（ ）A、矩形 B、菱形 C、对角线互相垂直的四边形 D、对角线相等的四边形8. 如图，正方形小方格边长为1，则网格中的△ABC是（ ）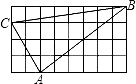
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对9. 如图，▱ABCD的周长为16cm，AC与BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（ ）
A、4cm B、6cm C、8cm D、10cm10. 下列命题中错误的是（ ）A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直 C、同旁内角互补 D、矩形的对角线相等11. 如图，在△ABC中，O是AC上一动点，过点O作直线MN∥BC．设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，若点O运动到AC的中点，且∠ACB=（ ）时，则四边形AECF是正方形．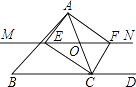
A、30° B、45° C、60° D、90°12. 如图，OP=1，过点P作PP1⊥OP且PP1=1，得OP1= ；再过点P1作P1P2⊥OP1且P1P2=1，得OP2= ；又过点P2作P2P3⊥OP2且P2P3=1，得OP3=2…依此法继续作下去，得OP2017=（ ）
A、 B、 C、 D、二、填空题
-
13. 如图，直角三角形ABC中∠ACB=90°，CD是高，∠A=30°，AB=4．则BD= ．
14. 某正n边形的一个内角为108°，则n= ．15. 直角三角形中两锐角平分线相交所成的角的度数是 ．16. 在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为17，AB=6，那么对角线AC+BD= ．17. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长=cm．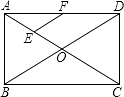
18.在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2017次后，顶点A在整个旋转过程中所经过的路程之和为 ．
三、解答题
-
19. 如图，在▱ABCD中，点E，F分别是边AD，BC的中点，求证：AF=CE．
20. 小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多了1m，当他把绳子的下端拉开5m后，发现下端刚好接触地面，求旗杆的高．
21.如图是4×4正方形网格，请在其中选取一个白色的单位正方形并涂黑，使图中黑色部分是一个中心对称图形．
22. 如图，点D、B分别在∠A的两边上，C是∠A内一点，且AB=AD，BC=DC，CE⊥AD，CF⊥AB，垂足分别为E、F．求证：CE=CF．
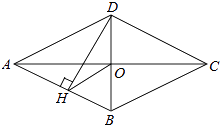
23. 如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DCO．
24. 如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．
(1)、求证：Rt△ADE与Rt△BEC全等；(2)、求证：△CDE是直角三角形．
