2017年河南省新乡市中考数学一模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
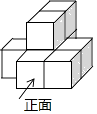
1. 下列各数中,最小的数是( )A、﹣ B、﹣1 C、﹣|﹣ | D、3﹣22. 大量事实证明,环境污染治理刻不容缓.据统计,全球每秒钟约有14.2万吨污水排入江河湖海.把14.2万用科学记数法表示为( )A、1.42×105 B、1.42×104 C、142×103 D、0.142×1063. 如图所示是8个完全相同的小正方体组成的几何体,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④5. 有15位同学参加一个知识竞赛活动,若他们比赛得分互不相同,且该竞赛共设8分获奖名额,甲同学知道自己的分数后,若要判断自己能否获奖,那么在15位同学成绩统计数据中,只要知道这组数据的( )A、平均数 B、中位数 C、众数 D、方差6. 如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )
4. 某同学做了四道题:①3m+4n=7mn;②(﹣2a2)3=﹣8a6;③6x6÷2x2=3x3;④y3•xy2=xy5 , 其中正确的题号是( )A、②④ B、①③ C、①② D、③④5. 有15位同学参加一个知识竞赛活动,若他们比赛得分互不相同,且该竞赛共设8分获奖名额,甲同学知道自己的分数后,若要判断自己能否获奖,那么在15位同学成绩统计数据中,只要知道这组数据的( )A、平均数 B、中位数 C、众数 D、方差6. 如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( ) A、∠CDB=∠BFD B、△BAC∽△OFD C、DF∥AC D、OD=BC7. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )
A、∠CDB=∠BFD B、△BAC∽△OFD C、DF∥AC D、OD=BC7. 如图,双曲线y= (x>0)经过线段AB的中点M,则△AOB的面积为( )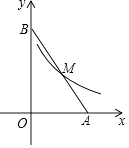 A、18 B、24 C、6 D、128. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
A、18 B、24 C、6 D、128. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( ) A、﹣1<x<5 B、x>5 C、x<﹣1 D、x<﹣1或x>59. 如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )
A、﹣1<x<5 B、x>5 C、x<﹣1 D、x<﹣1或x>59. 如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( ) A、 B、3 C、 D、10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A、 B、3 C、 D、10. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )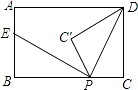 A、
A、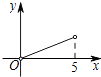 B、
B、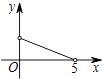 C、
C、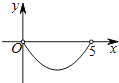 D、
D、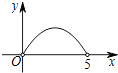
二、填空题
-
11. |﹣3|0+ = .12. 写一个你喜欢的整数m的值,使关于x的一元二次方程x2﹣3x+2m=0有两个不相等的实数根,m= .13. 用m、n、p、q四把钥匙去开A、B两把锁,其中仅有钥匙m能打开锁A,仅有钥匙n能打开锁B,则“取一把钥匙恰能打开一把锁”的概率是 .14. 如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= .
 15. 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE时,△EGH为等腰三角形.
15. 如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD折叠,使得点B落在边AD上,记为点G,BC的对应边GI与边CD交于点H,折痕为EF,则AE时,△EGH为等腰三角形.
三、解答题
-
16. 先化简( ﹣ )÷ 然后代入合适的x值求值,整数x满足﹣ .17. 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.
 (1)、求证:DE是⊙O的切线.(2)、填空:
(1)、求证:DE是⊙O的切线.(2)、填空:①当∠CAB=时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .
18. 数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长( ,要求结果精确得到0.1m) 19. 在平面直角坐标系内,双曲线:y= (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.
19. 在平面直角坐标系内,双曲线:y= (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD. (1)、求出双曲线的解析式;(2)、连结CD,求四边形OCDB的面积.20. 2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:
(1)、求出双曲线的解析式;(2)、连结CD,求四边形OCDB的面积.20. 2016年11月13日巴基斯坦瓜达尔港正式开港,此港成为我国“一带一路”必展战略上的一颗璀璨的明星,某大型远洋运输集团有三种型号的远洋货轮,每种型号的货轮载重量和盈利情况如下表所示:甲
乙
丙
平均货轮载重的吨数(万吨)
10
5
7.5
平均每吨货物可获例如(百元)
5
3.6
4
(1)、若用乙、丙两种型号的货轮共8艘,将55万吨的货物运送到瓜达尔港,问乙、丙两种型号的货轮各多少艘?(2)、集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内,并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量,如果设丙型货轮有m艘,则甲型货轮有艘,乙型货轮有艘(用含有m的式子表示),那么如何安排装运,可使集团获得最大利润?最大利润的多少?21. 如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.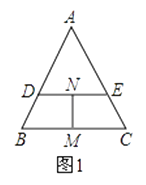 (1)、发现:在图1中, =;(2)、应用:如图2,将△ADE绕点A旋转,请求出 的值;
(1)、发现:在图1中, =;(2)、应用:如图2,将△ADE绕点A旋转,请求出 的值; (3)、拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 的值.
(3)、拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 的值. 22. 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
22. 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D. (1)、求该抛物线的函数关系式;(2)、当△ADP是直角三角形时,求点P的坐标;(3)、在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数关系式;(2)、当△ADP是直角三角形时,求点P的坐标;(3)、在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.