2016-2017学年山东省滨州市阳信县八年级下学期期中数学试卷
试卷更新日期:2017-07-24 类型:期中考试
一、选择题.
-
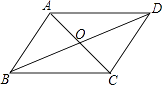
1. 下列运算中错误的是( )A、 + = B、 ÷ =2 C、 × = D、(﹣ )2=32. 如图,平行四边形ABCD的对角线AC、BD相交于点O,则下列说法一定正确的( )
 A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB3. 下列二次根式中,不能与合并的是( )A、2 B、 C、 D、4. 下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )A、a=3,b=4,c=5 B、a=5,b=12,c=13 C、a=1,b=2,c= D、a= ,b=2,c=35. 若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )A、60 B、30 C、20 D、326. 如果x≥1,那么化简 的结果是 .7. 顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )A、正方形 B、矩形 C、菱形 D、梯形8. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( )
A、AO=OD B、AO⊥OD C、AO=OC D、AO⊥AB3. 下列二次根式中,不能与合并的是( )A、2 B、 C、 D、4. 下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )A、a=3,b=4,c=5 B、a=5,b=12,c=13 C、a=1,b=2,c= D、a= ,b=2,c=35. 若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )A、60 B、30 C、20 D、326. 如果x≥1,那么化简 的结果是 .7. 顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )A、正方形 B、矩形 C、菱形 D、梯形8. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M表示的实数为( ) A、2.5 B、 C、 D、 ﹣19. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于( )
A、2.5 B、 C、 D、 ﹣19. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于( ) A、1 B、2 C、3 D、410. 已知实数x,y满足 +x2+4y2=4xy,则(x﹣y)2017的值为( )A、0 B、﹣1 C、1 D、201611. 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连结EF.若EF=2 ,BD=8,则菱形ABCD的周长为( )
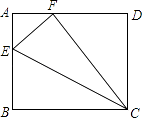
A、1 B、2 C、3 D、410. 已知实数x,y满足 +x2+4y2=4xy,则(x﹣y)2017的值为( )A、0 B、﹣1 C、1 D、201611. 如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连结EF.若EF=2 ,BD=8,则菱形ABCD的周长为( ) A、8 B、8 C、16 D、812. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE= ,其中正确的结论的个数为( )
A、8 B、8 C、16 D、812. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE= ,其中正确的结论的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 在直角坐标系中,已知点A (0,2),B(1,3),则线段AB的长度是 .14. 一个正方形的面积是5,那么这个正方形的对角线的长度为 .15. 已知x= +1,y= ﹣1,则x2﹣y2的值为 .16. 如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则AF的长为 .
 17. 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).
17. 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).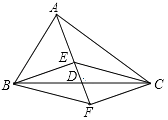 18. 如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
18. 如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
三、解答题
-
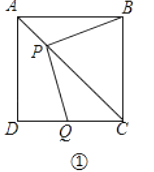
19. 根据问题进行计算:(1)、计算: × ﹣4× ×(1﹣ )0;(2)、已知三角形两边长为3,5,要使这个三角形是直角三角形,求出第三边的长.20. 如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.
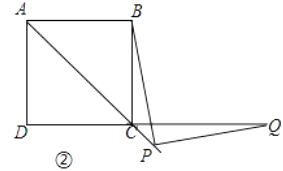
 21. 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
21. 某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口 小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? 22. 已知 = ,且x为奇数,求(1+x)• 的值.
22. 已知 = ,且x为奇数,求(1+x)• 的值.