2016-2017学年山东省临沂市河东区八年级下学期期中数学试卷
试卷更新日期：2017-07-24 类型：期中考试
一、选择题
-
1. 式子 在实数范围内有意义，则x的取值范围是（ ）A、x=0 B、x≥0 C、x＞﹣4 D、x≥﹣42. 用下列各组线段为边，能构成直角三角形的是（ ）A、1cm，2cm，3cm B、 cm， cm， cm C、1cm，2cm， cm D、2cm，3cm，4cm3. 下列二次根式中，是最简二次根式的是（ ）A、2 B、 C、 D、4. 把直角三角形两直角边同时扩大到原来的2倍，则斜边扩大到原来的（ ）A、2倍 B、4倍 C、3倍 D、5倍5. 如图，在菱形ABCD中，AB=5，∠BCD=120°，则对角线AC等于（ ）
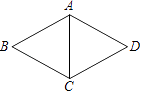A、20 B、15 C、10 D、56. 如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开．若测得AM的长为1.2km，则M，C两点间的距离为（ ）
A、0.5 km B、0.6 km C、0.9 km D、1.2 km7. 已知y= ，则 的值为（ ）A、 B、﹣ C、 D、﹣8. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（ ）
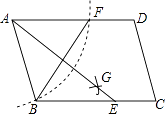A、4 B、6 C、8 D、109. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（ ）
A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE10.用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是（ ）
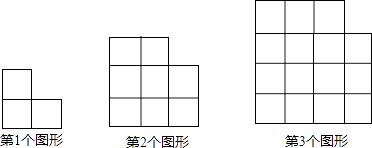A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣211.如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（ ）
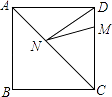A、6 B、8 C、12 D、10二、填空题
-
12. 在实数范围内因式分解：3m2﹣6= ．13. 如图所示，有一条小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是 m2 ．
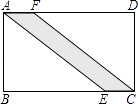14. 如图，四边形ABCD是平行四边形，AC与BD相交于点O，添加一个条件： ， 可使它成为菱形．
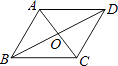15. 在△ABC中，AB=15，AC=13，高AD=12，则BC的长 ．16. 如图，延长正方形ABCD的边AB到E，使BE=AC，则∠E=度．
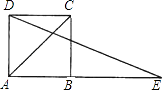17. 如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= BD，连接DM、DN、MN．若AB=6，则DN= ．
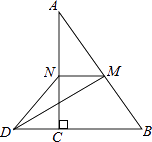18.如图，有一圆柱体，它的高为8cm，底面周长为12cm．在圆柱的下底面A点处有一个蜘蛛，它想吃到上底面上与A点相对的B点处的苍蝇，需要爬行的最短路径是 cm．
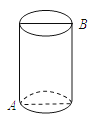19. 观察下列等式：第1个等式：a1= = ﹣1，
第2个等式：a2= = ，
第3个等式：a3= =2﹣ ，
第4个等式：a4= = ﹣2，
…
按上述规律，计算a1+a2+a3+…+an= ．
三、解答题
-
20. 已知x=2﹣ ，y=2+ ，求下列代数式的值：(1)、x2+2xy+y2；(2)、x2﹣y2 ．21. 如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AC上，这时梯足B到墙底端C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？
22. 如图，已知四边形ABCD是矩形，对角线AC，BD交于点O，CE∥BD，DE∥AC，CE与DE交于点E，请探索DC与OE的位置关系，并说明理由．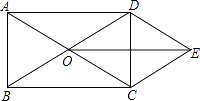
23. 如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．
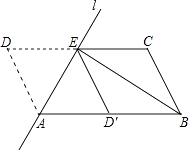(1)、求证：四边形BCED′是平行四边形；(2)、若BE平分∠ABC，求证：AB2=AE2+BE2 ．24. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
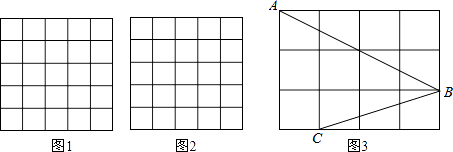(1)、在图1中以格点为顶点画一个面积为10的正方形；(2)、在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 ， ；(3)、如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．25. 如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．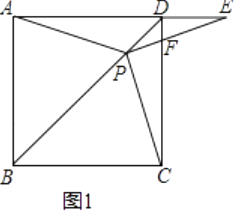
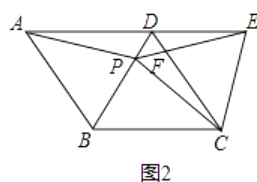(1)、证明：PC=PE；(2)、求∠CPE的度数；(3)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．