2017年河南省三门峡市中考数学一模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{\sqrt{2}}{2}$ 的倒数是（）

A、﹣ $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 改革开放以来，我国国内生产总值由2006年的3645亿元增长到2016年的300 670亿元．将300 670用科学记数法表示应为（）

A、0.30067×10⁶ B、3.0067×10⁵ C、3.0067×10⁴ D、30.067×10⁴

查看试题解析
3. 如图是婴儿车的平面示意图，其中AB∥CD，∠1=120°，∠3=40°，那么∠2的度数为（）

A、80° B、90° C、100° D、102°

查看试题解析
4. 小明因流感在医院观察，要掌握他在一周内的体温是否稳定，则医生需了解小明7天体温的（）

A、众数 B、方差 C、平均数 D、频数

查看试题解析
5. 几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是（）

A、4 B、5 C、6 D、7

查看试题解析
6. 若关于x的一元二次方程（k﹣1）x²+2x﹣2=0有不相等实数根，则k的取值范围是（）

A、k＞ $\frac{1}{2}$ B、k≥ $\frac{1}{2}$ C、k＞ $\frac{1}{2}$ 且k≠1 D、k≥ $\frac{1}{2}$ 且k≠1

查看试题解析
7. 一个袋子中装有3个红球和2个黄球，这些球的形状、大小、质地完全相同，在看不到球的条件下，随机从袋中摸出2个球，其中2个球颜色不相同的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{1}{5}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
8. 如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（）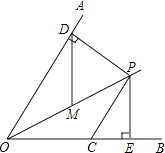

A、2 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
9. 如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（ $\sqrt{2}$ ， $\sqrt{2}$ ），弦AB经过点P，则图中阴影部分面积的最小值等于（）

A、2π﹣4 B、4π﹣8 C、 $\frac{8 π - 6 \sqrt{3}}{3}$ D、 $\frac{16 π - 12 \sqrt{3}}{3}$

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0，②当﹣1≤x≤3时，y＜0；③3a+c=0；④若（x₁ ， y₁）（x₂、y₂）在函数图象上，当0＜x₁＜x₂时，y₁＜y₂ ，其中正确的是（）

A、①②④ B、①③ C、①②③ D、①③④

查看试题解析

二、填空题

11. 如果代数式 $\frac{\sqrt{x + 1}}{x - 2}$ 有意义，那么字母x的取值范围是

查看试题解析
12. 如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC，若∠BAC和∠BOC互补，则弦BC的长度为．

查看试题解析
13. 如图所示，AB∥CD∥EF，AC与BD相交于点E，若CE=4，CF=3，AE=BC，则 $\frac{C D}{A B}$ 的值是．

查看试题解析
14.
如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（7，3），点E在边AB上，且AE=1，已知点P为y轴上一动点，连接EP，过点O作直线EP的垂线段，垂足为点H，在点P从点F（0， $\frac{25}{4}$ ）运动到原点O的过程中，点H的运动路径长为．

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连结AD，将△ACD沿AD折叠，点C落在点C′，连结C′D交AB于点E，连结BC′．当△BC′D是直角三角形时，DE的长为．

查看试题解析

三、解答题

16. 先化简，再求值：（ $\frac{a - 1}{a^{2} - 4 a + 4} - \frac{a + 2}{a^{2} - 2 a}$ ）÷（ $\frac{4}{a}$ ﹣1），其中a是满足不等组 ${\begin{matrix} 7 - a > 2 \\ 2 a > 3 \end{matrix}$ 的整数解．

查看试题解析
17. 小明在学习了数据的收集、整理与描述后，为妈妈整理记录了10月份的家庭支出情况，并绘制成如下尚不完整的统计图表，请你根据图表信息完成下列各题：
项目
物业费
伙食费
服装费
其他费
金额/元
800
400

(1)、10月份小明家共支出多少元？

(2)、在扇形统计图中，表示“其他费”的扇形圆心角为多少度？

(3)、请将表格补充完整；
项目
物业费
伙食费
服装费
其他费
金额/元
800
400

(4)、请将条形统计图补充完整．

查看试题解析
18.
如图所示，某工程队准备在山坡（山坡视为直线l）上修一条路，需要测量山坡的坡度，即tanα的值．测量员在山坡P处（不计此人身高）观察对面山顶上的一座铁塔，测得塔尖C的仰角为31°，塔底B的仰角为26.6°．已知塔高BC=40米，塔所在的山高OB=240米，OA=300米，图中的点O、B、C、A、P在同一平面内．求：

(1)、P到OC的距离．

(2)、山坡的坡度tanα．
（参考数据sin26.6°≈0.45，tan26.6°≈0.50；sin31°≈0.52，tan31°≈0.60）

查看试题解析
19. 随着柴静纪录片《穹顶之下》的播出，全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了A，B两种型号的空气净化器，已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元，用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同．

(1)、求一台A型空气净化器和一台B型空气净化器的进价各为多少元？

(2)、在销售过程中，A型空气净化器因为净化能力强，噪音小而更受消费者的欢迎．为了增大B型空气净化器的销量，商社电器决定对B型空气净化器进行降价销售，经市场调查，当B型空气净化器的售价为1800元时，每天可卖出4台，在此基础上，售价每降低50元，每天将多售出1台，如果每天商社电器销售B型空气净化器的利润为3200元，请问商社电器应将B型空气净化器的售价定为多少元？

查看试题解析
20. 在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y= $\frac{k}{x}$ （k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= $\frac{4}{3}$ ，点B的坐标为（m，﹣2）．

(1)、求△AHO的周长；

(2)、求该反比例函数和一次函数的解析式．

查看试题解析
21. 如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．

(1)、若AC=6，BC=10，求⊙O的半径．

(2)、过点E作弦EF⊥AB于M，连接AF，若∠AFE=2∠ABC，求证：四边形ACEF是菱形．

查看试题解析
22. 在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合），以AD为边在AD的右侧作正方形ADEF，连接CF．

(1)、
观察猜想：如图（1），当点D在线段BC上时，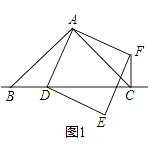
①BC与CF的位置关系是：；
②BC、CD、CF之间的数量关系为：（将结论直接写在横线上）

(2)、
数学思考：如图（2），当点D在线段CB的延长线上时，上述①、②中的结论是否仍然成立？若成立，请给予证明，若不成立，请你写出正确结论再给予证明．

查看试题解析
23.
如图，抛物线y=ax²﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A坐标为（4，0）．

(1)、求该抛物线的解析式；

(2)、抛物线的顶点为N，在x轴上找一点K，使CK+KN最小，并求出点K的坐标；

(3)、点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；

(4)、若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

项目	物业费	伙食费	服装费	其他费
金额/元	800			400

项目	物业费	伙食费	服装费	其他费
金额/元	800			400