2017年河南省普通高中中考数学模拟试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣1 $\frac{1}{2}$ 的倒数的绝对值是（）

A、 $\frac{2}{3}$ B、﹣1 $\frac{1}{2}$ C、1 $\frac{1}{2}$ D、 $- \frac{2}{3}$

查看试题解析
2. 京剧是我国的国粹，是介绍、传播中国传统艺术文化的重要媒介．在下面的四个京剧脸谱中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 中科院国家天文台直尺建设，位于贵州省平塘县的世界最大单口经射电望远镜﹣500米口径球面射电望远镜于2016年9月全部建成并初步投入使用，它是世界上现役的最具威力的单天线射电望远镜，理论上说，该射电望远镜能接收到137亿光念以外的电磁信号，这个距离接近于宇宙的边缘，将137亿用科学记数法表示为（）

A、1.37×10¹¹ B、1.37×10¹² C、1.37×10⁹ D、1.37×10¹⁰

查看试题解析
4. 某同学做了四道题：①3m+4n=7mn；②（﹣2a²）³=﹣8a⁶；③6x⁶÷2x²=3x³；④y³•xy²=xy⁵ ，其中正确的题号是（）

A、②④ B、①③ C、①② D、③④

查看试题解析
5. 如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
6. 用m，n，p，q四把钥匙去开A，B两把锁，其中仅有钥匙m能打开锁A，仅有钥匙n能打开锁B，则“取一把钥匙恰能打开一把锁”的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{8}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
7. 如图，双曲线y= $\frac{6}{x}$ （x＞0）经过线段AB的中点M，则△AOB的面积为（）

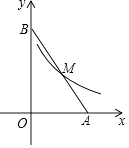A、18 B、24 C、6 D、12

查看试题解析
8. 对于一组数据：10，17，15，10，18，20，下列说法错误的是（）

A、中位数是16 B、方差是 $\frac{41}{3}$ C、众数是10 D、平均数是15

查看试题解析
9. 如图，△ABC中，∠C=90°，∠A=30°，BC=2，按照如下步骤作图：①分别以点A，B为圆心，大于线段AB长度的一半为半径画弧，两弧分别相交于点M，N；②作直线MN分别交AB，AC于点D，E，连结BE，则BE的长是（）

A、 $\frac{4 \sqrt{3}}{3}$ B、3 C、 $\sqrt{5}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
10.
如图，点A（2，0），B（0，2），将扇形AOB沿x轴正方向做无滑动的滚动，在滚动过程中点O的对应点依次记为点O₁ ，点O₂ ，点O₃…，则O₁₀的坐标是（）

A、（16+4π，0） B、（14+4π，2） C、（14+3π，2） D、（12+3π，0）

查看试题解析

二、填空题

11. |﹣3|⁰+ $\sqrt[3]{- 8}$ = ．

查看试题解析
12. 如图，已知AD平分∠CAB，DE∥AC，∠1=30°，则∠2=°．

查看试题解析
13. 已知抛物线y=ax²﹣4ax﹣5a，其中a＜0，则不等式ax²﹣4ax﹣5a＞0的解集是．

查看试题解析
14. 如图，菱形ABCD，∠A=60°，AB=4，以点B为圆心的扇形与边CD相切于点E，扇形的圆心角为60°，点E是CD的中点，图中两块阴影部分的面积分别为S₁ ， S₂ ，则S₂﹣S₁= ．

查看试题解析
15. 如图，矩形ABCD中，AB=8，AD=6，将矩形ABCD折叠，使得点B落在边AD上，记为点G，BC的对应边GI与边CD交于点H，折痕为EF，则AE=时，△EGH为等腰三角形．

查看试题解析

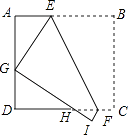
三、解答题

16. 先化简，再求值：（ $\frac{m}{m - 2}$ ﹣ $\frac{4}{m^{2} - 2 m}$ ）÷ $\frac{m + 2}{m^{2} - m}$ ，其中m在数轴上对应的点到原点的距离不大于2，且m是整数．

查看试题解析
17. 如图，在△ABC中，AB=AC，点O为边AB的中点，OD⊥BC于点D，AM⊥BC于点M，以点O为圆心，线段OD为半径的圆与AM相切于点N．

(1)、求证：AN=BD；

(2)、填空：点P是⊙O上的一个动点，
①若AB=4，连结OC，则PC的最大值是；
②当∠BOP=时，以O，D，B，P为顶点四边形是平行四边形．

查看试题解析
18.
2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队，携多架歼﹣15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务，在某次演习中，预警直升机A发现在其北偏东60°，距离160千米处有一可疑目标B，预警直升机立即向位于南偏西30°距离40千米处的航母C报告，航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去，请求出舰载战斗机到达目标的航程BC．
（结果保留整数，参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3， $\sqrt{3}$ ≈1.73）

查看试题解析
19. 在平面直角坐标系内，双曲线：y= $\frac{k}{x}$ （x＞0）分别与直线OA：y=x和直线AB：y=﹣x+10，交于C，D两点，并且OC=3BD．

(1)、求出双曲线的解析式；

(2)、连结CD，求四边形OCDB的面积．

查看试题解析
20. 2016年11月13日巴基斯坦瓜达尔港正式开港，此港成为我国“一带一路”必展战略上的一颗璀璨的明星，某大型远洋运输集团有三种型号的远洋货轮，每种型号的货轮载重量和盈利情况如下表所示：

甲
乙
丙
平均货轮载重的吨数（万吨）
10
5
7.5
平均每吨货物可获例如（百元）
5
3.6
4

(1)、若用乙、丙两种型号的货轮共8艘，将55万吨的货物运送到瓜达尔港，问乙、丙两种型号的货轮各多少艘？

(2)、集团计划未来用三种型号的货轮共20艘装运180万吨的货物到国内，并且乙、丙两种型号的货轮数量之和不超过甲型货轮的数量，如果设丙型货轮有m艘，则甲型货轮有艘，乙型货轮有艘（用含有m的式子表示），那么如何安排装运，可使集团获得最大利润？最大利润的多少？

查看试题解析
21.
如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．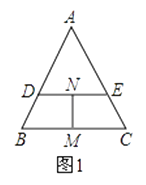

(1)、发现：在图1中， $\frac{M N}{B D}$ =；

(2)、
应用：如图2，将△ADE绕点A旋转，请求出 $\frac{M N}{B D}$ 的值；

(3)、
拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N分别是底边BC，DE的中点，若BD⊥CE，请直接写出 $\frac{M N}{B D}$ 的值．

查看试题解析
22.
如图1，在平面直角坐标系中，直线y=﹣x+1与抛物线y=ax²+bx+c（a≠0）相交于点A（1，0）和点D（﹣4，5），并与y轴交于点C，抛物线的对称轴为直线x=﹣1，且抛物线与x轴交于另一点B．

(1)、求该抛物线的函数表达式；

(2)、若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；

(3)、
如图2，若点M是直线x=﹣1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．

查看试题解析

	甲	乙	丙
平均货轮载重的吨数（万吨）	10	5	7.5
平均每吨货物可获例如（百元）	5	3.6	4