2016-2017学年重庆市重点中学八年级下学期期中数学试卷（B卷）

试卷更新日期：2017-07-24 类型：期中考试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是（　　）

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 下列根式中能与 $\sqrt{3}$ 合并的二次根式为（）

A、 $\sqrt{\frac{3}{2}}$ B、 $\sqrt{24}$ C、 $\sqrt{12}$ D、 $\sqrt{0.5}$

查看试题解析
3. 下列长度的三条线段能组成直角三角形的是（）

A、1，1， $\sqrt{2}$ B、2，3，4 C、4，5，6 D、6，8，11

查看试题解析
4. 下列变形中，正确的是（）

A、（2 $\sqrt{3}$ ）²=2×3=6 B、 $\sqrt{{(- \frac{2}{5})}^{2}}$ =﹣ $\frac{2}{5}$ C、 $\sqrt{9 + 16}$ = $\sqrt{9} + \sqrt{16}$ D、 $\sqrt{(- 9) \times (- 4)}$ = $\sqrt{9} \times \sqrt{4}$

查看试题解析
5. 如图，在平行四边形ABCD中，AC，BD为对角线，BC=6，BC边上的高为4，则图中阴影部分的面积为（）

A、3 B、6 C、12 D、24

查看试题解析
6. 杨伯家小院子的四棵小树E、F、G、H刚好在其梯形院子ABCD各边的中点上，若在四边形EFGH种上小草，则这块草地的形状是（）

A、平行四边形 B、矩形 C、正方形 D、菱形

查看试题解析
7. 如图，在△ABC中，∠A=45°，∠B=30°，CD⊥AB，垂足为D，AD=1，则BD的长为（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{3}$ D、3

查看试题解析
8. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了（）步路（假设2步为1米），却踩伤了花草．

A、1 B、2 C、3 D、4

查看试题解析
9. 如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（）

A、8cm B、5 $\sqrt{2}$ cm C、5.5cm D、1cm

查看试题解析
10. 如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=8，则四边形CODE的周长（）

A、8 B、12 C、16 D、20

查看试题解析
11. 如图，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A₁B₁C₁D₁；把正方形A₁B₁C₁D₁边长按原法延长一倍得到正方形A₂B₂C₂D₂；以此进行下去…，则正方形A_nB_nC_nD_n的面积为（）

A、（ $\sqrt{5}$ ）ⁿ B、5ⁿ C、5ⁿ^﹣¹ D、5ⁿ⁺¹

查看试题解析
12.
如图，菱形ABCD的边长为4，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，则EF+BF的最小值是（）

A、4 B、2 $\sqrt{3}$ C、4 $\sqrt{3}$ D、2 $\sqrt{7}$

查看试题解析

二、填空题

13. 若二次根式 $\sqrt{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
14. 计算： $\sqrt[3]{27} - 4 \sqrt{\frac{1}{2}} + \sqrt{8}$ = ．

查看试题解析
15. 如图，▱ABCD的对角线AC，BD相交于点O，点E是CD的中点，△ABD的周长为16cm，则△DOE的周长是 cm．

查看试题解析
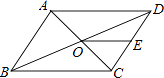16. 已知a，b为直角三角形的两条直角边的长，且a，b满足|a﹣3|+ $\sqrt{b - 5}$ =0，则此三角形的周长为．

查看试题解析
17. 如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为m．

查看试题解析
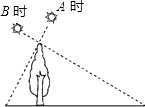18. 如图，菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EG⊥CD于点G，则∠FGC= ．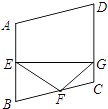

查看试题解析

三、解答题．

19. 计算：

(1)、 $\sqrt{8}$ +|1﹣ $\sqrt{2}$ |﹣π⁰+（ $\frac{1}{2}$ ）^﹣¹

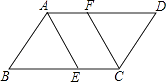
(2)、（2 $\sqrt{5}$ ﹣2 $\sqrt{3}$ ）（ $\sqrt{12}$ + $\sqrt{20}$ ）

查看试题解析
20. 如图，已知ABCD是平行四边形，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F．求证：AF=EC．

查看试题解析

四、解答题

21. 先化简，再求值 $\frac{1}{x + 1} - \frac{1}{x^{2} - 1} \div \frac{x + 1}{x^{2} - 2 x + 1}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
22. 交通安全是社会关注的热点问题，安全隐患主要是超速和超载．某中学八年级数学活动小组的同学进行了测试汽车速度的实验．如图，先在笔直的公路1旁选取一点P，在公路1上确定点O、B，使得PO⊥l，PO=100米，∠PBO=45°．这时，一辆轿车在公路1上由B向A匀速驶来，测得此车从B处行驶到A处所用的时间为3秒，并测得∠APO=60°．此路段限速每小时80千米，试判断此车是否超速？请说明理由（参考数据： $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）．

查看试题解析
23. 如图是一块地的平面图，AD=4m，CD=3m，AB=13m，BC=12m，∠ADC=90°，求这块地的面积．

查看试题解析
24. 先阅读下列材料，再解决问题：
阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去一层根号．
例如： $\sqrt{3 + 2 \sqrt{2}}$ = $\sqrt{3 + 2 \times 1 \times \sqrt{2}}$ = $\sqrt{1^{2} + {(\sqrt{2})}^{2} + 2 \times 1 \times \sqrt{2}}$ = $\sqrt{{(1 + \sqrt{2})}^{2}}$ =|1+ $\sqrt{2}$ |=1+ $\sqrt{2}$

(1)、解决问题：
模仿上例的过程填空：
$\sqrt{14 + 6 \sqrt{5}}$ = $\sqrt{14 + 2 \times 3 \times \sqrt{5}}$ ====

(2)、根据上述思路，试将下列各式化简．
① $\sqrt{28 - 10 \sqrt{3}}$ ② $\sqrt{1 + \frac{\sqrt{3}}{2}}$ ．

查看试题解析

五、解答题

25. 如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：

(1)、如果AB=AC，∠BAC=90°，
①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为，数量关系为．
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

(2)、如果AB≠AC，∠BAC≠90°点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？并说明理由．

查看试题解析
26.
将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动 $\frac{2}{3}$ 秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．

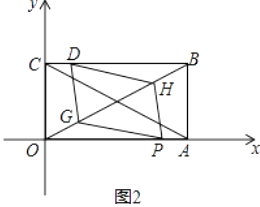(1)、求点B的坐标，并用含t的代数式表示OP，OQ；

(2)、当t=1时，如图1，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；

(3)、在（2）的条件下，矩形对角线AC，BO交于M，取OM中点G，BM中点H，求证：当t=1时四边形DGPH是平行四边形．

查看试题解析